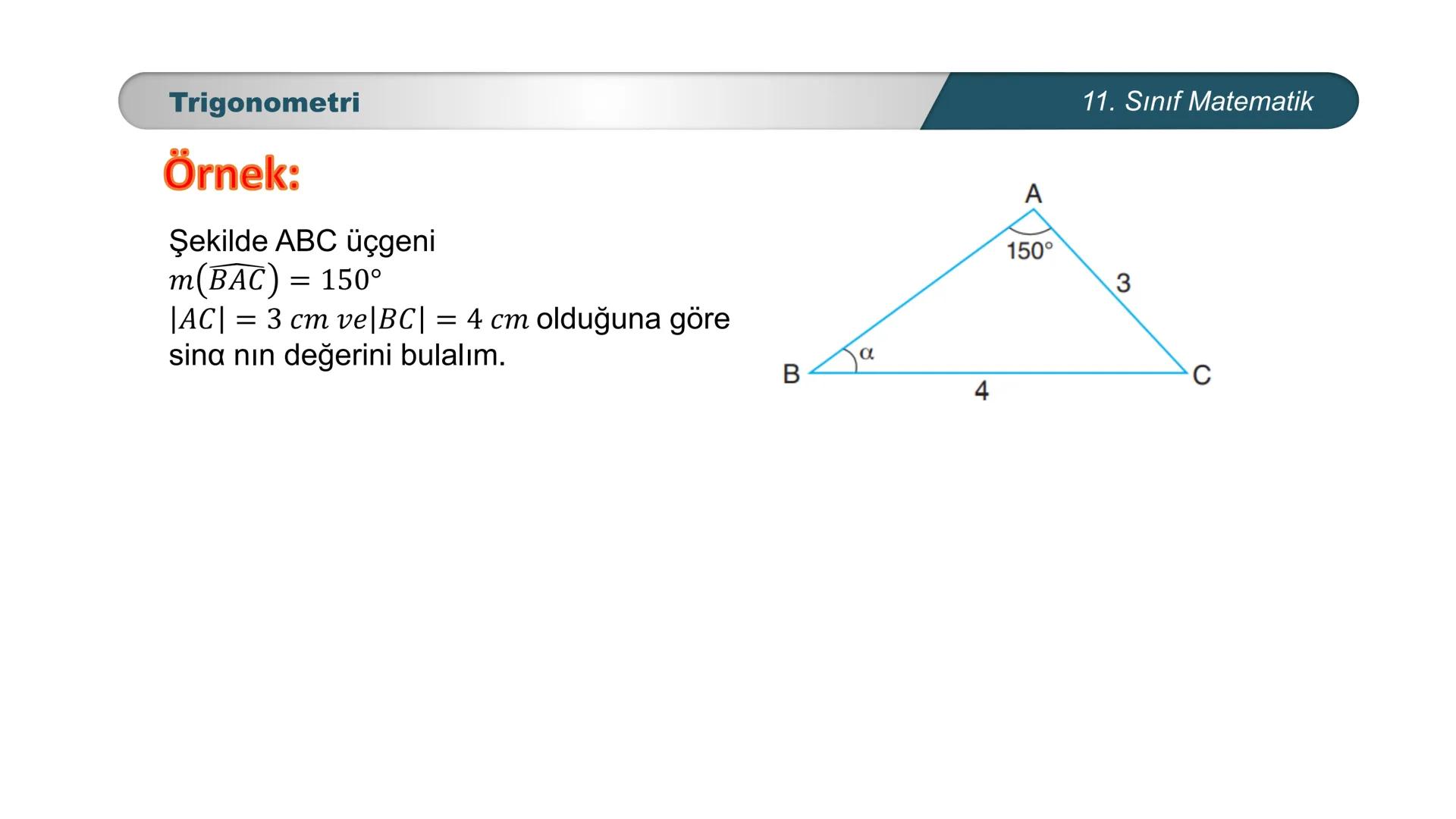
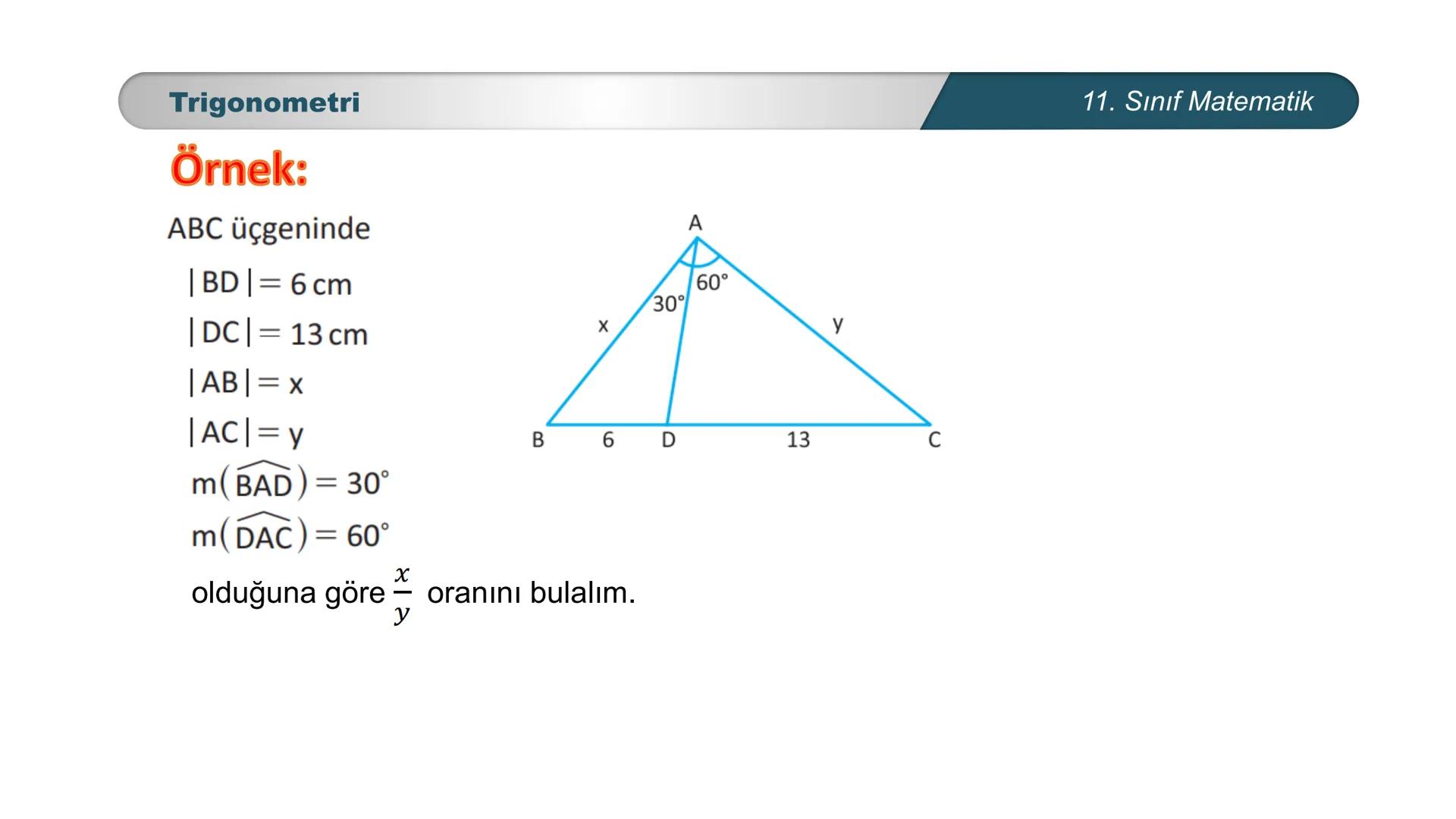
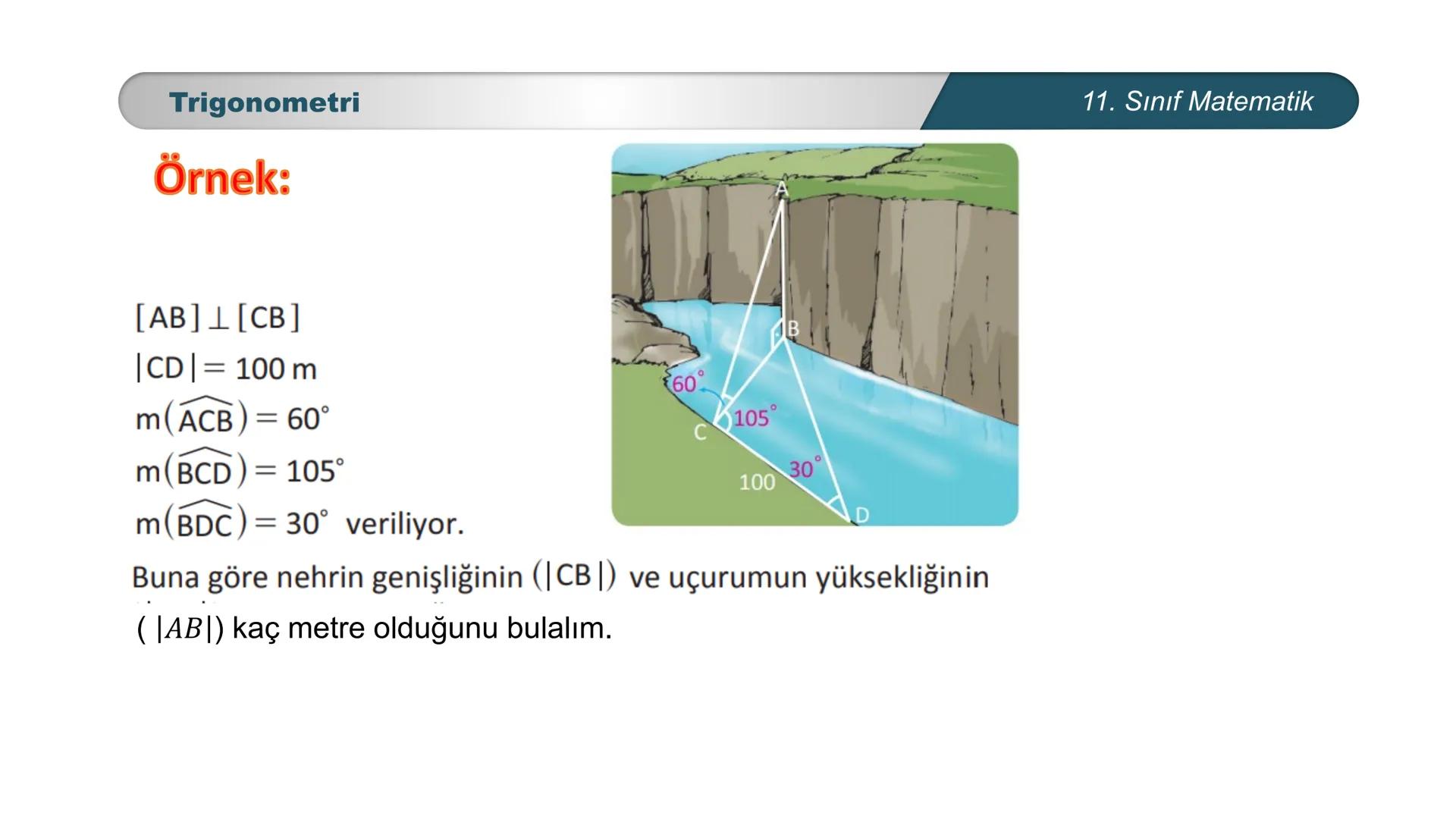
Sinüs Teoremi

Trigonometrinin en kullanışlı teoremlerinden biri olan sinüs teoremi, üçgenlerdeki kenar-açı ilişkilerini anlamamızı sağlar. Bu teorem, günlük hayattaki birçok ölçüm ve hesaplama probleminde karşımıza çıkar.

Sinüs teoremi, 11. sınıf matematik müfredatının önemli bir parçasıdır ve üçgenlerdeki bilinmeyen kenar ve açıları hesaplamak için kullanılır.

Not: Sinüs teoremi, bilinen iki açı ve bir kenardan veya iki kenar ve bir açıdan yola çıkarak bilinmeyen değerleri hesaplamamıza olanak tanır.

Sinüs Teoreminin Tanımı

Sinüs teoremi, bir üçgende her kenarın uzunluğunun, karşısındaki açının sinüs değerine oranının eşit olduğunu söyler. Yani ABC üçgeninin kenar uzunlukları a, b, c olmak üzere:

$\frac{a}{\sin\hat{A}} = \frac{b}{\sin\hat{B}} = \frac{c}{\sin\hat{C}}$

Bu formül, üçgenin herhangi bir açısını veya kenarını bulmak için kullanılabilir. Örneğin, iki açı ve bir kenar biliniyorsa diğer kenarlar hesaplanabilir.

Sinüs teoremi, özellikle dik açılı olmayan üçgenlerde çok kullanışlıdır ve navigasyon, mimari ve mühendislik gibi alanlarda pratik uygulamaları vardır.

İpucu: Formülü şöyle de hatırlayabilirsin: Kenarların karşı açıların sinüslerine oranı sabittir.

İspat

Sinüs teoreminin matematiksel ispatı, üçgenin alanını farklı şekillerde ifade etmeye dayanır. Bir ABC üçgeninin alanını sinüslü alan formülü ile yazarsak:

$A(ABC) = \frac{b \cdot c \cdot \sin A}{2} = \frac{a \cdot c \cdot \sin B}{2} = \frac{a \cdot b \cdot \sin C}{2}$

Bu eşitliğin her tarafını 2 ile çarparsak:

$b \cdot c \cdot \sin A = a \cdot c \cdot \sin B = a \cdot b \cdot \sin C$

Şimdi bu eşitliği $a \cdot b \cdot c$ ile bölersek:

$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$

Bu eşitliği çapraz çarparak bildiğimiz sinüs teoremi formülüne ulaşırız:

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Dikkat: İspatın özü, üçgenin alanını farklı şekillerde yazabilmemizdir - bu yaklaşım birçok trigonometri teoreminin ispatında kullanılır!

Sinüs Teoremi Örnek 1

Bir ABC üçgeninde |AB| = 8 birim, |AC| = 4√2 birim ve m(∠ACB) = 45° verilmiş. B açısının ölçüsünü bulalım.

Sinüs teoremini uygulayalım:

$\frac{|AB|}{\sin(∠ACB)} = \frac{|AC|}{\sin(∠ABC)}$

Verilen değerleri yerleştirirsek:

$\frac{8}{\sin 45°} = \frac{4\sqrt{2}}{\sin(∠ABC)}$

$\frac{8}{\frac{\sqrt{2}}{2}} = \frac{4\sqrt{2}}{\sin(∠ABC)}$

$\frac{8 \cdot 2}{\sqrt{2}} = \frac{4\sqrt{2}}{\sin(∠ABC)}$

$\frac{16}{\sqrt{2}} = \frac{4\sqrt{2}}{\sin(∠ABC)}$

Buradan sin(∠ABC) değerini çözersek B açısının ölçüsünü bulabiliriz.

Püf Noktası: Sinüs teoremini kullanırken, her zaman karşılıklı kenar-açı ikililerini eşleştirdiğinizden emin olun!

Sinüs Teoremi Örnek 2

ABC üçgeninde |AC| = 10 cm, m(∠BAC) = 75°, m(∠ABC) = 60° verilmiş. |AB| = x değerini bulalım.

Öncelikle, üçgenin iç açıları toplamı 180° olduğundan: m(∠BCA) = 180° - 75° - 60° = 45°

Şimdi sinüs teoremini uygulayalım:

$\frac{|AB|}{\sin(∠BCA)} = \frac{|AC|}{\sin(∠ABC)}$

$\frac{x}{\sin 45°} = \frac{10}{\sin 60°}$

$\frac{x}{\frac{\sqrt{2}}{2}} = \frac{10}{\frac{\sqrt{3}}{2}}$

$\frac{2x}{\sqrt{2}} = \frac{20}{\sqrt{3}}$

Bu denklemden x değerini çözeriz.

Hatırlatma: Üçgenin iç açıları toplamının 180° olduğunu unutma! Bilinmeyen bir açıyı bu şekilde kolayca hesaplayabilirsin.

Sinüs Teoremi Örnek 3

Bir ABC üçgeninde m(∠BAC) = 150°, |AC| = 3 cm ve |BC| = 4 cm verilmiş. sin α değerini bulalım.

Burada α açısı ∠ABC olarak tanımlanmıştır. Üçgenin iç açıları toplamı 180° olduğundan: m(∠ABC) + m(∠BCA) + 150° = 180° m(∠ABC) + m(∠BCA) = 30°

Sinüs teoremini uygulayalım:

$\frac{|AB|}{\sin(∠BCA)} = \frac{|AC|}{\sin(∠ABC)} = \frac{|BC|}{\sin(∠BAC)}$

$\frac{|AC|}{\sin(∠ABC)} = \frac{|BC|}{\sin(∠BAC)}$

$\frac{3}{\sin α} = \frac{4}{\sin 150°}$

sin 150° = sin$180° - 30°$ = sin 30° = 1/2 olduğunu hatırlarsak:

$\frac{3}{\sin α} = \frac{4}{1/2} = 8$

Buradan sin α değerini çözebiliriz.

İpucu: Açı değerlerini bilmiyorsan, sinüs teoremi kenar uzunluklarını kullanarak açıları bulmana yardımcı olabilir!

Sinüs Teoremi Örnek 4

ABC üçgeninde |BD| = 6 cm, |DC| = 13 cm, |AB| = x, |AC| = y, m(∠BAD) = 30°, m(∠DAC) = 60° verilmiş. x/y oranını bulalım.

Bu soruda ABC üçgeninde D noktası, BC kenarı üzerinde bir noktadır. ABD ve ADC üçgenlerini ayrı ayrı düşünelim.

ABD üçgeninde sinüs teoremini uygularsak:

$\frac{|AB|}{\sin(∠ADB)} = \frac{|BD|}{\sin(∠BAD)}$

$\frac{x}{\sin(∠ADB)} = \frac{6}{\sin 30°}$

ADC üçgeninde sinüs teoremini uygularsak:

$\frac{|AC|}{\sin(∠ADC)} = \frac{|DC|}{\sin(∠DAC)}$

$\frac{y}{\sin(∠ADC)} = \frac{13}{\sin 60°}$

∠ADB ve ∠ADC açıları arasındaki ilişkiyi kullanarak x/y oranını bulabiliriz.

Öneri: Karmaşık üçgen problemlerinde, üçgeni daha küçük parçalara ayırmak çözümü kolaylaştırabilir!

Sinüs Teoremi Örnek 5

ABC üçgeninde m(∠A) = 30° ve |BC| = 6 cm verilmiş. $\frac{\sin B + \sin C}{|AB| + |AC|}$ oranını bulalım.

İlk olarak, sinüs teoremini kullanarak |AB| ve |AC| değerlerini |BC| ve açılar cinsinden ifade edelim:

$\frac{|AB|}{\sin C} = \frac{|BC|}{\sin A} \Rightarrow |AB| = \frac{|BC| \cdot \sin C}{\sin A} = \frac{6 \cdot \sin C}{\sin 30°}$

$\frac{|AC|}{\sin B} = \frac{|BC|}{\sin A} \Rightarrow |AC| = \frac{|BC| \cdot \sin B}{\sin A} = \frac{6 \cdot \sin B}{\sin 30°}$

Bu ifadeleri istenen orana yerleştirip, sin 30° = 1/2 olduğunu kullanarak sadeleştirelim. Ayrıca üçgenin iç açıları toplamının 180° olduğunu unutmayalım.

Matematiksel İncelik: Bazen doğrudan sonuç aramak yerine, bilinenleri kullanarak bilinmeyenleri ifade etmek ve sonra sadeleştirmek daha kolay olabilir.

Sinüs Teoremi Örnek 6

Kenar uzunlukları a, b, c cm olan ABC üçgeninde, $\frac{\sin B}{\sin C} = \frac{2}{3}$, b + c = 15 cm ve m(∠A) = 60° olduğuna göre a değerini bulalım.

Sinüs teoremini kullanarak:

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Buradan: $\frac{b}{\sin B} = \frac{c}{\sin C}$

$\frac{b}{c} = \frac{\sin B}{\sin C} = \frac{2}{3}$

Yani b = $\frac{2c}{3}$

b + c = 15 cm olduğundan: $\frac{2c}{3} + c = 15$ $\frac{5c}{3} = 15$ $c = 9$ ve $b = 6$ bulunur.

Şimdi a değerini sinüs teoreminden bulabiliriz: $\frac{a}{\sin 60°} = \frac{c}{\sin C}$

Strateji: Önce verilen oranı kullanarak kenarlar arasındaki ilişkiyi bulmak, karmaşık problemleri basamak basamak çözmenin anahtarıdır.

Sinüs Teoremi Örnek 7

ABC üçgeninin çevre uzunluğu 24 cm ve $\frac{|BC|}{\sin A} = 10$ olduğuna göre, $\sin A + \sin B + \sin C$ toplamını bulalım.

Sinüs teoremini kullanarak:

$\frac{|AB|}{\sin C} = \frac{|BC|}{\sin A} = \frac{|AC|}{\sin B} = 10$

Buradan: $|BC| = 10 \sin A$ $|AB| = 10 \sin C$ $|AC| = 10 \sin B$

Üçgenin çevresi: $|AB| + |BC| + |AC| = 24$ $10 \sin C + 10 \sin A + 10 \sin B = 24$ $10(\sin A + \sin B + \sin C) = 24$ $\sin A + \sin B + \sin C = \frac{24}{10} = 2.4$

Güzel Bir Gözlem: Sinüs teoremi kullanılarak üçgenin çevresi ile açıların sinüsleri arasında ilginç bir ilişki ortaya çıkmıştır. Bu tür bağlantıları fark etmek matematik anlayışını derinleştirir.