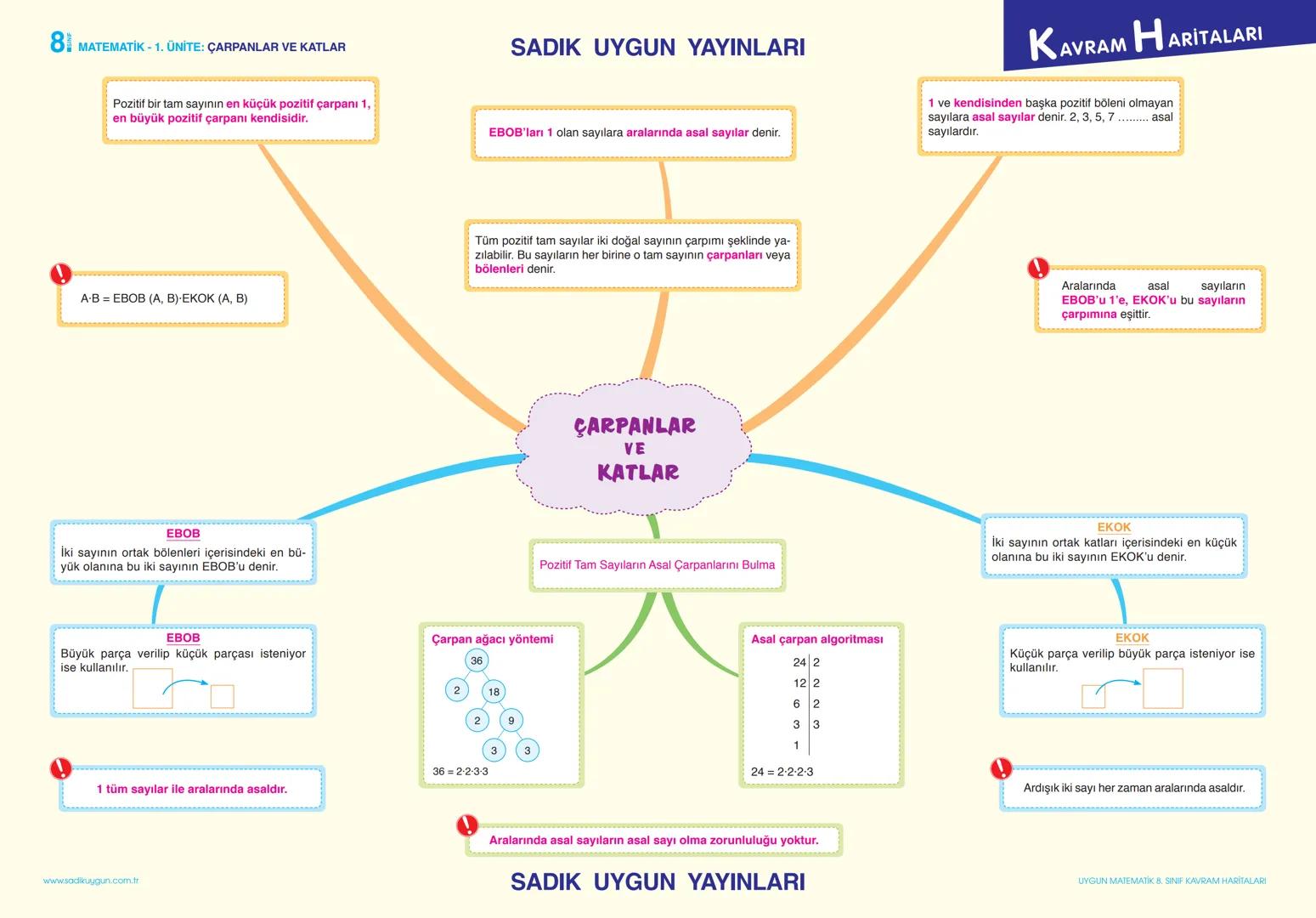
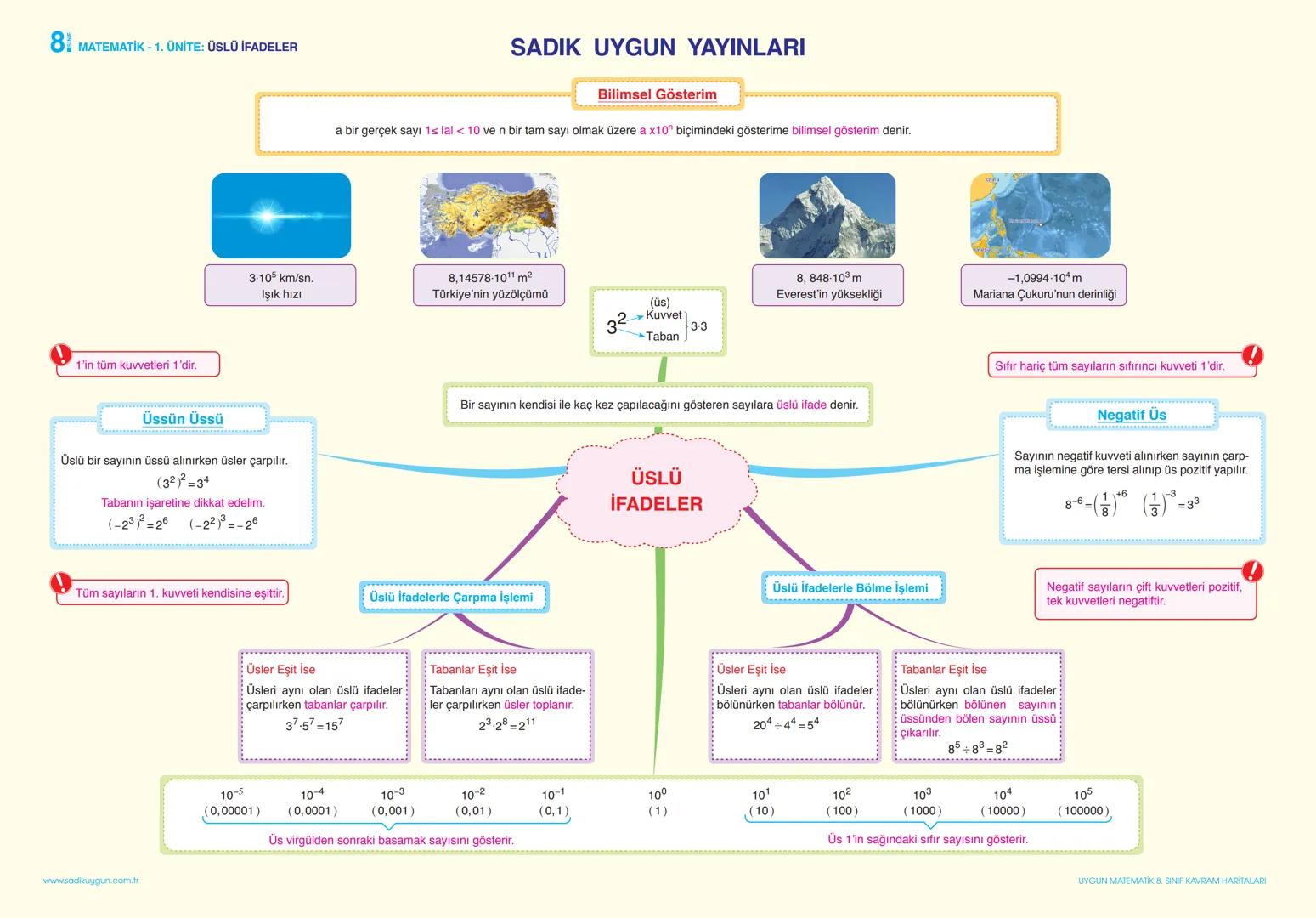
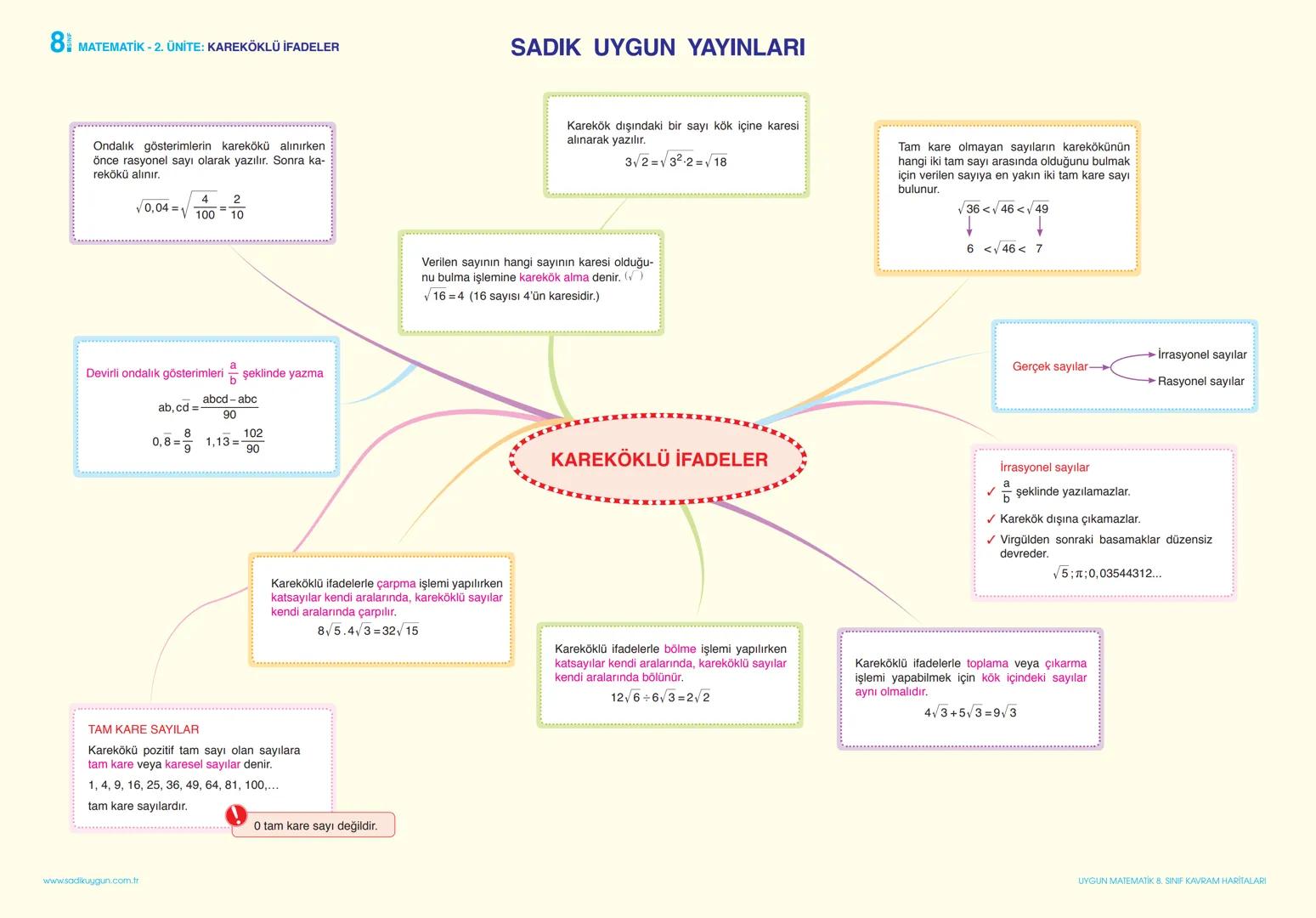
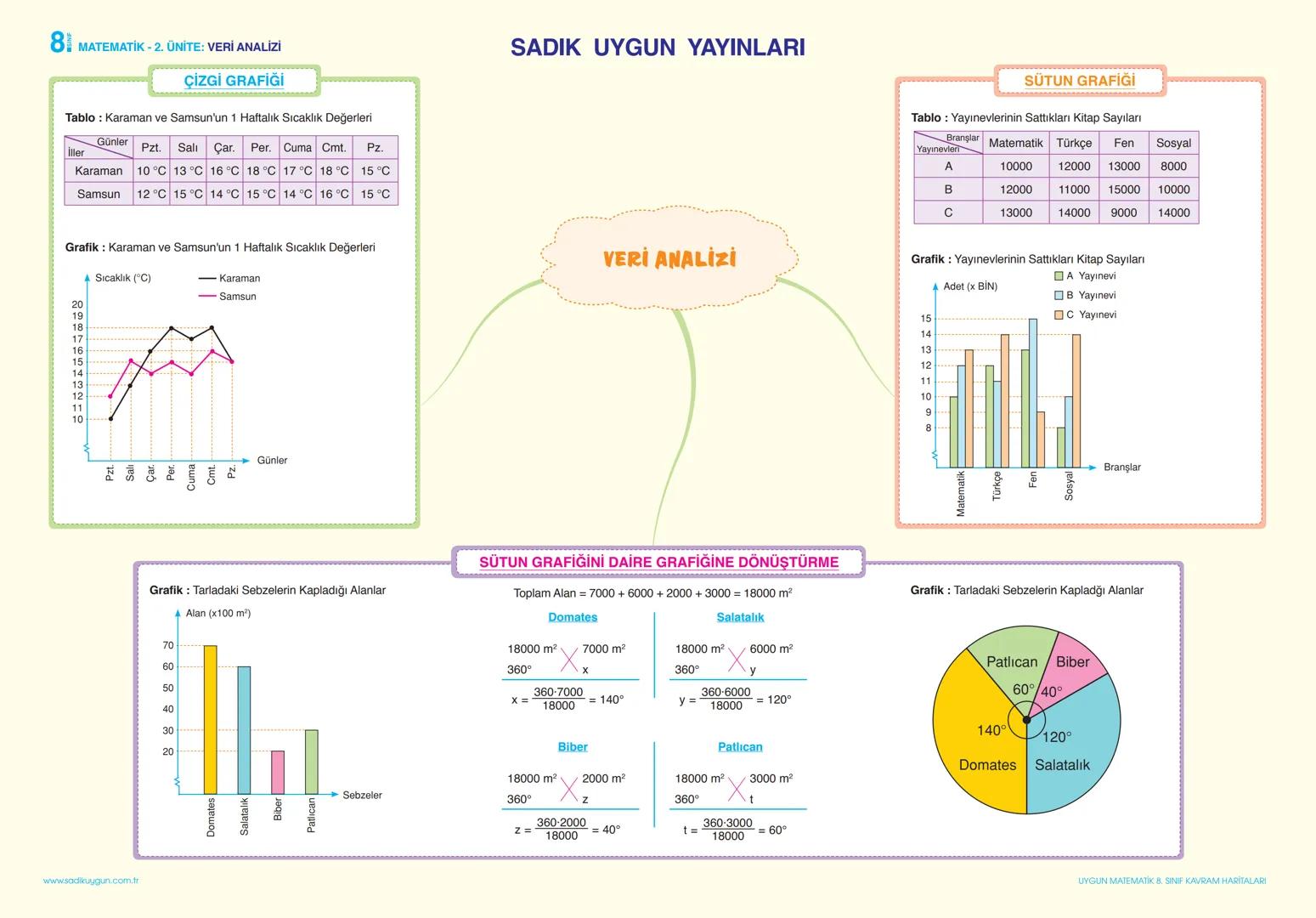
Basit Olayların Olma Olasılığı
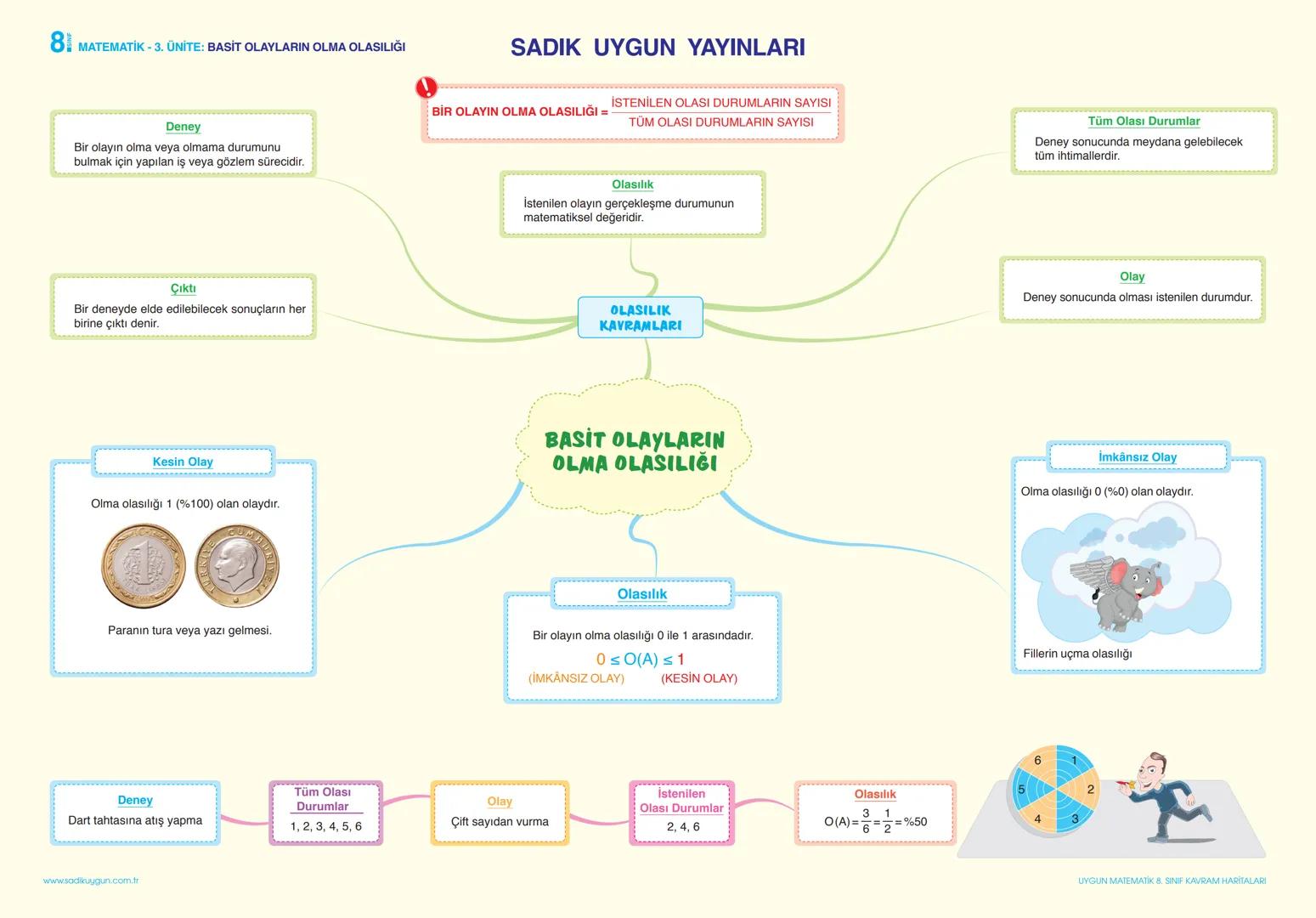
Olasılık günlük hayatta sürekli karşılaştığımız belirsizlikleri matematiksel olarak ifade etmemizi sağlar. Bir para atışında yazı gelme olasılığı 1/2 = %50'dir!
Olasılık formülü: P(A) = İstenilen durumların sayısı ÷ Tüm olası durumların sayısı. Olasılık değeri her zaman 0 ile 1 arasındadır. 0 imkansız olay, 1 ise kesin olay anlamına gelir.
Bir zar atışında çift sayı gelme olasılığı: İstenilen durumlar {2,4,6} = 3 adet, tüm durumlar {1,2,3,4,5,6} = 6 adet. Dolayısıyla P = 3/6 = 1/2 = %50'dir.
💡 Günlük yaşam: Hava durumu tahminleri, spor müsabakası sonuçları, sınav başarısı gibi birçok durumda olasılık hesaplamaları kullanılır!