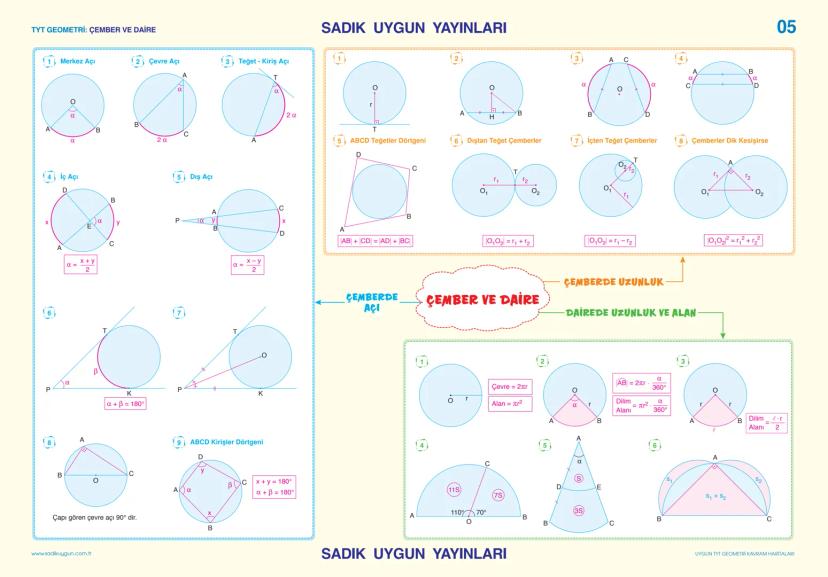
Analitik Geometri - Dönüşümler ve Vektörler
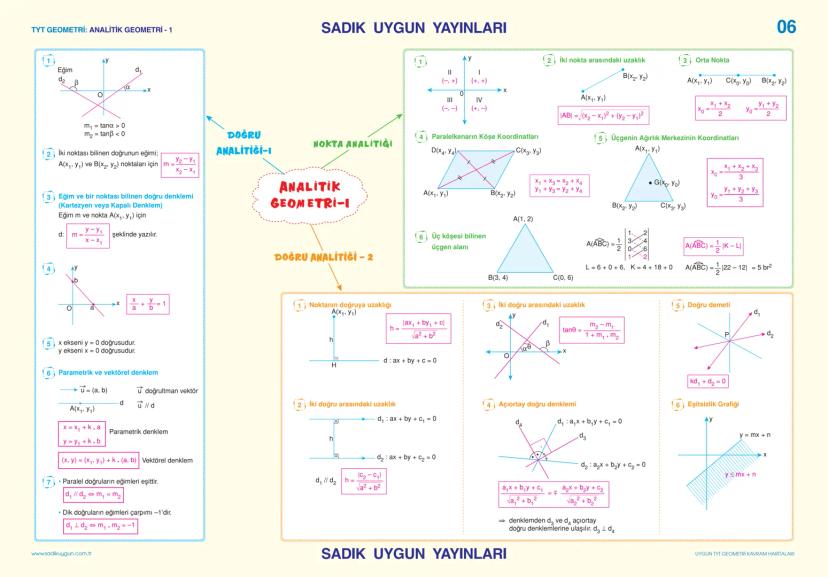
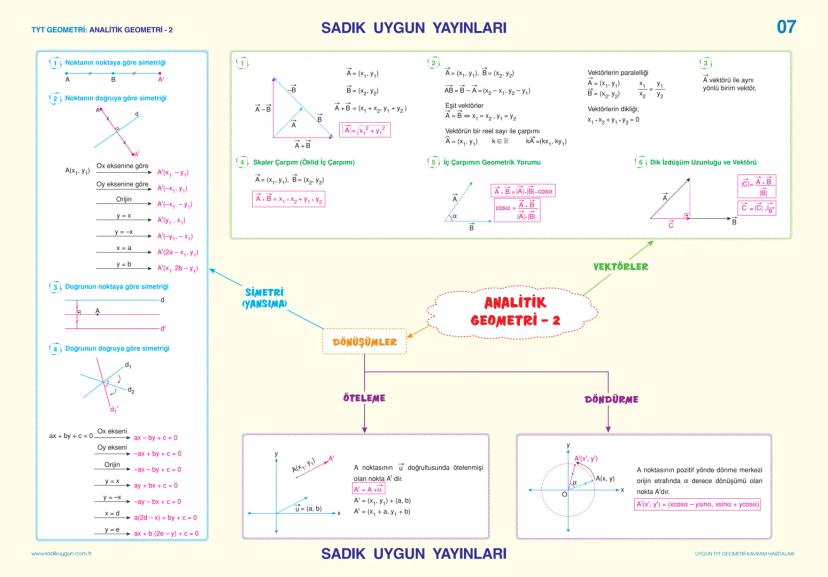
Simetri işlemleri sınavda çok soruluyor. Ox eksenine göre A(x,y) → A'x,−y, Oy eksenine göre A(x,y) → A'−x,y. Orijine göre simetri A(x,y) → A'−x,−y.
Vektörler konusunda toplama A + B = x1+x2,y1+y2, skaler çarpım kA = (kx₁, ky₁). İç çarpım A·B = x₁x₂ + y₁y₂, geometrik yorumu A·B = |A|·|B|·cosα.
Öteleme işleminde A' = A + u şeklinde. Döndürme için orijin etrafında α açısı kadar: A'(x',y') = xcosα−ysinα,xsinα+ycosα.
Vektör uzunluğu |A| = √x2+y2 formülü ile hesaplanır. İki vektör dik ise iç çarpımları sıfırdır.
Önemli: y = x doğrusuna göre simetride A(x,y) → A'(y,x) olur.
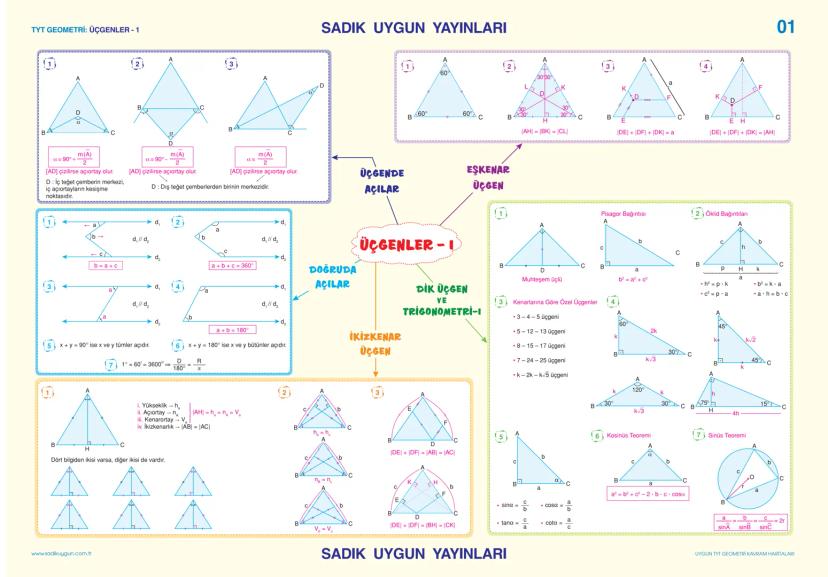

![TYT GEOMETRİ: ÜÇGENLER - 1
SADIK UYGUN YAYINLARI
01
2
(3)
KA
D
3
F
a
KA
D
K
D
F
Da
BA
C
B
$\alpha$=90°+
m(A)
2
[AD] çiz](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0193c223-a25b-75d7-a0a9-b7ca73190c3e_image_page_1.webp&w=2048&q=75)
![TYT GEOMETRİ: ÜÇGENLER - 1
SADIK UYGUN YAYINLARI
01
2
(3)
KA
D
3
F
a
KA
D
K
D
F
Da
BA
C
B
$\alpha$=90°+
m(A)
2
[AD] çiz](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0193c223-a25b-75d7-a0a9-b7ca73190c3e_image_page_2.webp&w=2048&q=75)
![TYT GEOMETRİ: ÜÇGENLER - 1
SADIK UYGUN YAYINLARI
01
2
(3)
KA
D
3
F
a
KA
D
K
D
F
Da
BA
C
B
$\alpha$=90°+
m(A)
2
[AD] çiz](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0193c223-a25b-75d7-a0a9-b7ca73190c3e_image_page_3.webp&w=2048&q=75)
![TYT GEOMETRİ: ÜÇGENLER - 1
SADIK UYGUN YAYINLARI
01
2
(3)
KA
D
3
F
a
KA
D
K
D
F
Da
BA
C
B
$\alpha$=90°+
m(A)
2
[AD] çiz](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0193c223-a25b-75d7-a0a9-b7ca73190c3e_image_page_4.webp&w=2048&q=75)
![TYT GEOMETRİ: ÜÇGENLER - 1
SADIK UYGUN YAYINLARI
01
2
(3)
KA
D
3
F
a
KA
D
K
D
F
Da
BA
C
B
$\alpha$=90°+
m(A)
2
[AD] çiz](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0193c223-a25b-75d7-a0a9-b7ca73190c3e_image_page_5.webp&w=2048&q=75)
![TYT GEOMETRİ: ÜÇGENLER - 1
SADIK UYGUN YAYINLARI
01
2
(3)
KA
D
3
F
a
KA
D
K
D
F
Da
BA
C
B
$\alpha$=90°+
m(A)
2
[AD] çiz](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0193c223-a25b-75d7-a0a9-b7ca73190c3e_image_page_6.webp&w=2048&q=75)
![TYT GEOMETRİ: ÜÇGENLER - 1
SADIK UYGUN YAYINLARI
01
2
(3)
KA
D
3
F
a
KA
D
K
D
F
Da
BA
C
B
$\alpha$=90°+
m(A)
2
[AD] çiz](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0193c223-a25b-75d7-a0a9-b7ca73190c3e_image_page_7.webp&w=2048&q=75)
![TYT GEOMETRİ: ÜÇGENLER - 1
SADIK UYGUN YAYINLARI
01
2
(3)
KA
D
3
F
a
KA
D
K
D
F
Da
BA
C
B
$\alpha$=90°+
m(A)
2
[AD] çiz](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0193c223-a25b-75d7-a0a9-b7ca73190c3e_image_page_8.webp&w=2048&q=75)