Üçgende Açılar ve Kenar Bağıntıları

Bir üçgende iç açıların toplamı her zaman 180°'dir ve dış açıların toplamı 360°'dir. Bu temel bilgi, birçok geometri problemini çözerken başlangıç noktanız olacak.

Üçgende açı-kenar bağıntıları çok önemlidir: Bir üçgende büyük açının karşısında büyük kenar, küçük açının karşısında küçük kenar bulunur. Üçgenin kenarları arasında da |b-c| < a < b+c gibi özel bağıntılar vardır.

Dik üçgende Pisagor Teoremi geçerlidir: a² = b² + c². Bir üçgende açılara göre özel durumlar vardır: Eğer açı 90°'den büyükse a² > b² + c², küçükse a² < b² + c² bağıntısı oluşur.

⭐ Bir üçgende kenarortay, açıortay ve yükseklikleri tanımayı öğren. "Muhteşem dörtlü" olan |BD| = |DC| = |AD| gibi özel bağıntılar ve özel açılı üçgenler $45°-45°-90° veya 30°-60°-90°$, problemleri hızlı çözmeni sağlayacak.

İkizkenar Üçgen ve Eşkenar Üçgen

İkizkenar üçgende iki kenar birbirine eşittir $|AB| = |AC|$. Bu eşitlik, üçgenin açıları ve özel doğruları arasında önemli bağlantılar oluşturur. Örneğin, eşit kenarların karşısındaki açılar da birbirine eşittir.

Eşkenar üçgende ise tüm kenarlar birbirine eşittir ve tüm iç açılar 60°'dir. Eşkenar üçgenin alanı a²√3/4 formülüyle bulunur.

Üçgende açıortay, bir açıyı iki eşit parçaya bölen doğru parçasıdır. Açıortay özellikleri problem çözümlerinde sıkça kullanılır. Kenarortay, bir köşeyi karşı kenarın orta noktasına birleştiren doğru parçasıdır.

Üçgende yükseklik, bir köşeden karşı kenara indirilen dik doğrudur. Üçgenin yükseklikleri bir noktada kesişir ve bu noktaya yüksekliklerin dikme merkezi denir.

🔍 İkizkenar ve eşkenar üçgenlerdeki özel formülleri ve nokta bağıntılarını iyi öğren! Örneğin "üçgende bir noktanın üç kenara uzaklıkları toplamı" veya "kenar ortayların kesiştiği ağırlık merkezi" gibi kavramlar sınavlarda çok soruluyor.

Üçgende Alan ve Benzerlik

Üçgenin alanını bulmanın birçok yolu vardır. Taban ve yükseklikle, A(ABC) = (a.h)/2 formülüyle hesaplayabilirsin. Ayrıca kenar uzunlukları biliniyorsa Heron formülü kullanılabilir: A(ABC) = √$u(u-a)(u-b)(u-c)$ $u = çevre/2$.

Üçgenin iç teğet çemberinin yarıçapını kullanarak da alan hesaplayabiliriz: A(ABC) = u.r (r iç teğet çemberinin yarıçapı). Çevrel çemberin yarıçapıyla da A(ABC) = (a.b.c)/(4R) formülü geçerlidir.

Benzerlik, geometrinin en güçlü kavramlarından biridir. İki üçgen arasında benzerlik, şu durumlarda sağlanır:

• Açı-Açı (A.A.) Benzerliği
• Kenar-Açı-Kenar Benzerliği
• Kenar-Kenar-Kenar Benzerliği

Benzer üçgenlerin karşılıklı kenarları orantılıdır ve alanlarının oranı benzerlik oranının karesidir. Thales Teoremi ve Menelaus Teoremi benzerlikle ilgili önemli teoremleridir.

💡 Benzerlik oranı "k" ise, benzer üçgenlerin çevrelerinin oranı k, alanlarının oranı k² olur. Bunu unutma ve sınav sorularında hızlıca kullan!

Doğrunun Analitik İncelenmesi

Koordinat düzleminde çalışmak, geometriyi cebirle birleştirmemizi sağlar. İki nokta arasındaki uzaklığı d = √$(x₂-x₁)² + (y₂-y₁)²$ formülüyle buluruz. Doğru parçasının orta noktası ise P = $(x₁+x₂)/2, (y₁+y₂)/2$ formülüyle hesaplanır.

Doğrunun eğimi, o doğrunun x-eksenine göre yükselme veya alçalma oranını gösterir: m = $y₂-y₁$/$x₂-x₁$. Eğim açısı α olan bir doğruda, m = tan(α) olur. Eğim pozitif ise doğru yukarı, negatif ise aşağı doğru gider.

Bir doğrunun denklemi farklı şekillerde ifade edilebilir:

• Eğim-kesme formu: y = mx + b
• Genel form: ax + by + c = 0
• İki noktalı form: $y-y₁$/$x-x₁$ = $y₂-y₁$/$x₂-x₁$

İki doğrunun birbirine göre durumları da önemlidir. Paralel doğruların eğimleri eşittir. Dik doğruların eğimlerinin çarpımı -1'dir. Bir noktanın bir doğruya uzaklığı d = |ax₀+by₀+c|/√$a²+b²$ formülüyle hesaplanır.

🔑 İki doğru arasındaki açıyı bulmak için tanα = |m₁-m₂|/$1+m₁.m₂$ formülünü kullan. Açıortay denklemlerini de öğrenmeyi unutma, analitik geometri sorularında işine çok yarayacak!

Dörtgenler

Dörtgenler, dört kenarı olan kapalı şekillerdir. Bir dörtgenin iç açılarının toplamı 360°dir, dış açılarının toplamı da 360°dir.

Dörtgenin alanını çeşitli yöntemlerle hesaplayabiliriz. Köşegenler kullanılarak A(ABCD) = (e.f.sinθ)/2 formülü uygulanır (e ve f köşegenlerin uzunlukları, θ aralarındaki açı). Köşegenlerin birbirini ortaladığı dörtgenlerde a² + c² = b² + d² bağıntısı geçerlidir.

Yamuk, karşılıklı kenarlarından yalnızca biri paralel olan dörtgendir. Yamuğun alanı A = $(a+c).h$/2 formülüyle hesaplanır (a ve c paralel kenarlar, h yükseklik). İkizkenar yamukta yan kenarlar eşit uzunluktadır.

Özel dörtgenlere dikkat etmelisin:

• Yamukta karşılıklı açıların toplamı 180°
• Dik yamukta bir iç açı 90°
• Paralelkenarda karşılıklı kenarlar paralel ve eşit
• Dikdörtgende tüm açılar 90°
• Eşkenar dörtgende tüm kenarlar eşit
• Karede tüm kenarlar eşit ve tüm açılar 90°

📐 Dörtgenin köşegenlerinin kesişim noktasındaki özellikler çok önemlidir. Paralelkenarda köşegenler birbirini ortalar. Eşkenar dörtgende köşegenler birbirine diktir. Karede köşegenler hem birbirine diktir hem de birbirini ortalar.

Paralelkenar, Dikdörtgen, Eşkenar Dörtgen ve Kare

Paralelkenar, karşılıklı kenarları paralel ve eşit olan dörtgendir. Paralelkenarda karşılıklı açılar eşittir ve köşegenler birbirini ortalar. Alanı A = a.h (a taban, h yükseklik) formülüyle bulunur.

Dikdörtgen, tüm açıları 90° olan paralelkenardır. Köşegen uzunlukları eşittir ve köşegen² = kenar1² + kenar2² bağıntısı vardır. Alanı A = a.b formülüyle hesaplanır.

Eşkenar dörtgen (deltoid), iki çift kenardan oluşan özel bir dörtgendir. Köşegenler birbirine diktir ve bir köşegen diğerini iki eşit parçaya böler. Alanı A = (e.f)/2 formülüyle bulunur (e ve f köşegenler).

Kare, tüm kenarları eşit ve tüm açıları 90° olan dörtgendir. Kareler hem dikdörtgen hem paralelkenar hem de eşkenar dörtgen özelliklerini taşır. Alanı A = a² formülüyle bulunur ve köşegenleri e = a.√2 uzunluğundadır.

⭐ Dikdörtgende |KD|² + |KB|² = |KA|² + |KC|² özelliği çok işine yarayacak. Bu özellik, dörtgenin dikdörtgen olup olmadığını test etmek için kullanılabilir.

Çokgenler

Çokgenler, kapalı düzlemsel şekillerdir. Konveks çokgenlerin iç açılarının toplamı $n-2$.180°, dış açılarının toplamı ise her zaman 360°'dir (n kenar sayısı). Bir çokgende köşegen sayısı n.$n-3$/2 formülüyle bulunur.

Düzgün konveks çokgenler, tüm kenar uzunlukları ve iç açıları eşit olan çokgenlerdir. Düzgün çokgenlerin önemli özellikleri:

• İç açı ölçüsü = $(n-2).180°$/n
• Dış açı ölçüsü = 360°/n
• Her düzgün çokgenin bir iç teğet çemberi ve bir çevrel çemberi vardır

Çift sayıda kenarı olan düzgün çokgenlerde karşılıklı kenarlar paraleldir. Tek sayıda kenarı olan düzgün çokgenlerde bir köşeden karşı kenara çizilen dikme hem kenarortay hem de açıortaydır.

Düzgün altıgen ve düzgün sekizgen gibi özel çokgenler, özel geometrik özellikler gösterir. Düzgün altıgenin bir iç açısı 120°, düzgün sekizgenin bir iç açısı 135°'dir.

🔍 Düzgün çokgenlerde, aynı sayıda köşeleri birleştiren köşegenlerin uzunlukları eşittir. Bu özellik, birçok çokgen sorusunu çözmenin anahtarıdır.

Çemberde Açılar

Çemberde açılar, geometri konusunun temel parçasıdır. Merkez açı, çember merkezinden geçen ve iki yarıçapın oluşturduğu açıdır. Çevre açı ise çember üzerindeki bir noktadan geçen ve iki kirişin oluşturduğu açıdır.

Aynı yayı gören merkez açı, çevre açının iki katıdır: α = 2α'. Aynı yayı gören çevre açıların ölçüleri birbirine eşittir. Özellikle, çap gören çevre açı 90°'dir.

Teğet-kiriş açısı, bir teğet ile bir kiriş arasında oluşan açıdır ve karşısındaki yayın ölçüsünün yarısına eşittir: θ = α/2. Ayrıca, aynı yay gören çevre açı ile teğet-kiriş açısının ölçüsü birbirine eşittir.

Çemberde kirişler dörtgeni, tüm köşeleri çember üzerinde olan dörtgendir. Bu dörtgende karşılıklı açıların toplamı 180°'dir: α + β = 180°.

⭐ Paralelogramın çember üzerindeki köşeleri oluşturabilmesi için dikdörtgen olması gerektiğini unutma. Çember üzerinde bir kirişler dörtgeni oluşturmak için dörtgenin karşılıklı açılarının tümler olması gerekir.

Çemberde Uzunluk ve Alan

Çemberde uzunluk hesaplarken, kirilerin ve teğetlerin özelliklerini kullanırız. Bir noktadan çembere çizilen en uzun kiriş, o noktadan geçen çap; en kısa kiriş ise noktayı çembere dik olarak bağlayan doğrudur.

Kuvvet kavramı, çemberde çok önemlidir. Eğer P noktasından çembere teğet çizilirse, |PT|² = |PA|.|PB| bağıntısı geçerlidir (T teğet noktası, A ve B çemberi kesen doğru parçasının kesim noktaları). Bu ilişkiye "bir noktanın çembere göre kuvveti" denir.

Çemberde alan hesabı, genellikle yay ve merkez açı kullanılarak yapılır. Daire diliminin alanı A = (πr²α)/360° formülüyle bulunur (α merkez açı derecesi). Daire parçasının alanı ise A = $r²(α-sin α)$/2 formülüyle hesaplanır.

Çemberde benzerlik oranları ve alan oranları da önemlidir. İki benzer şeklin alanlarının oranı, benzerlik oranının karesidir.

🔑 Çembere dıştan çizilen teğetlerin uzunlukları eşittir. Bu özellik, çember sorularında sıkça kullanılır ve problemleri çözmeyi kolaylaştırır.

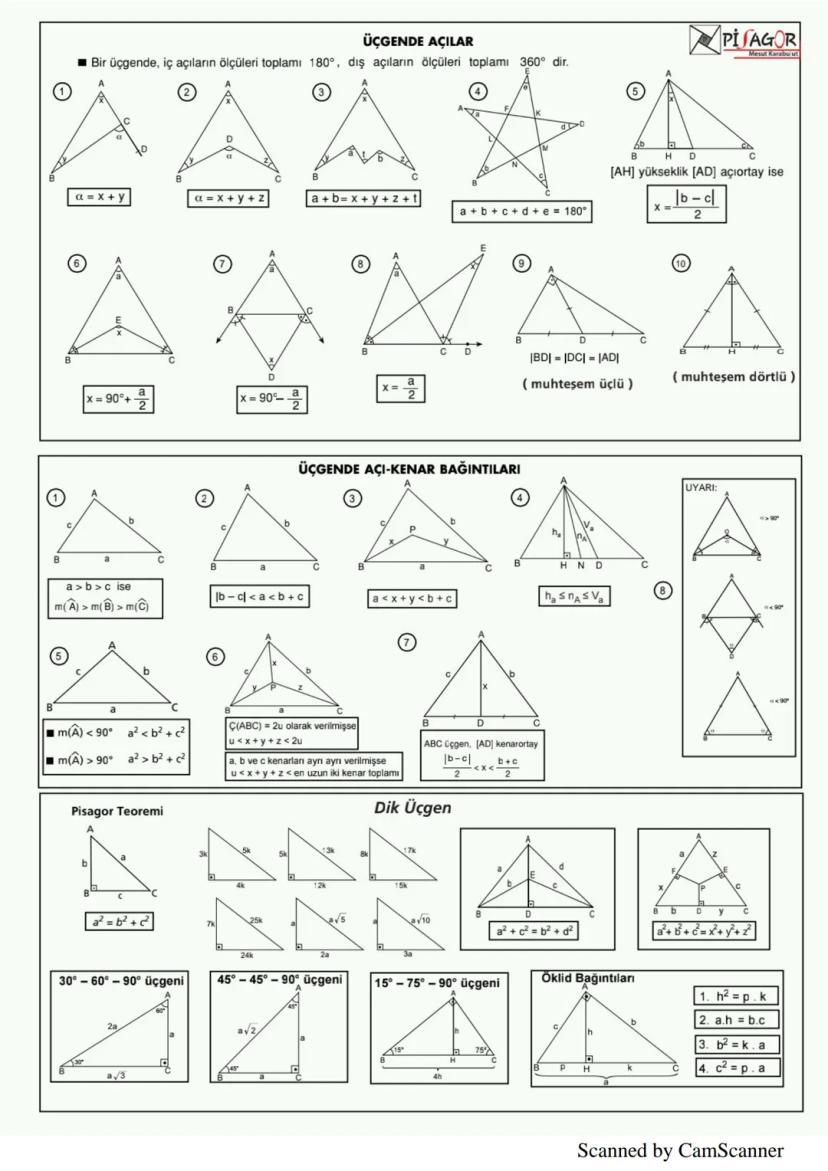
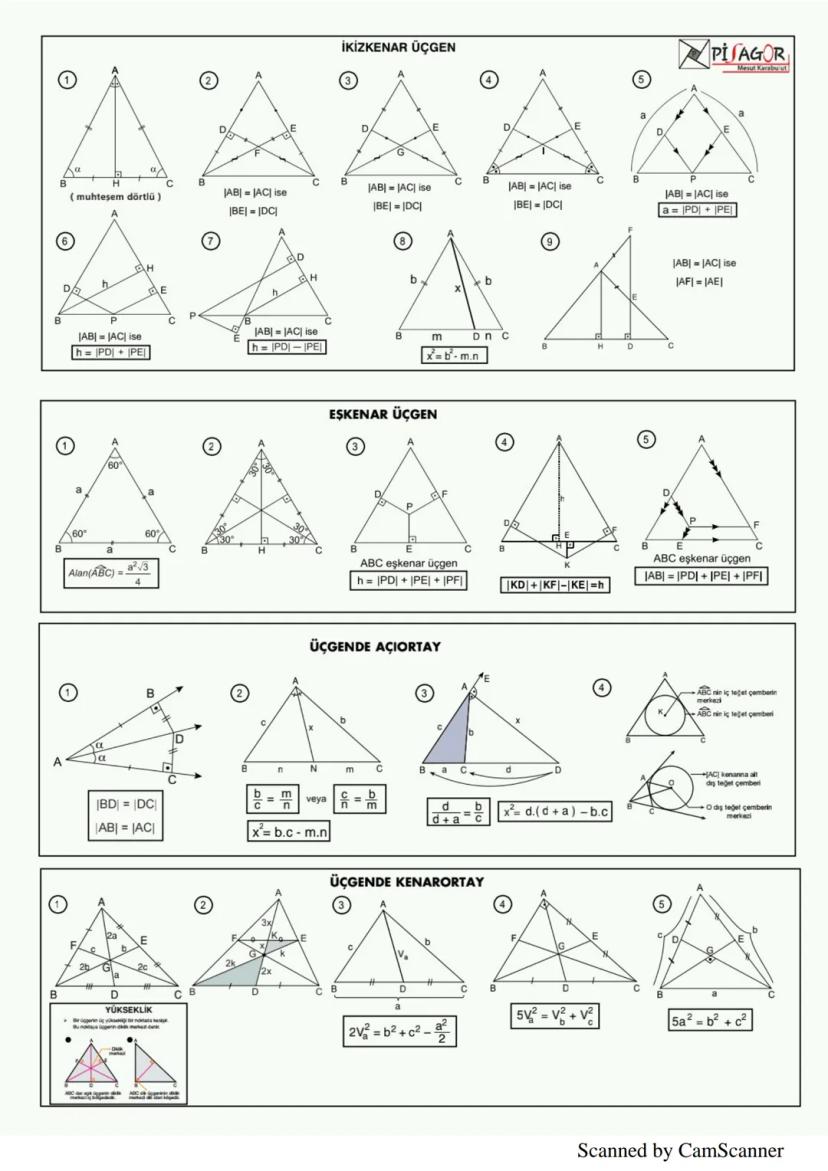
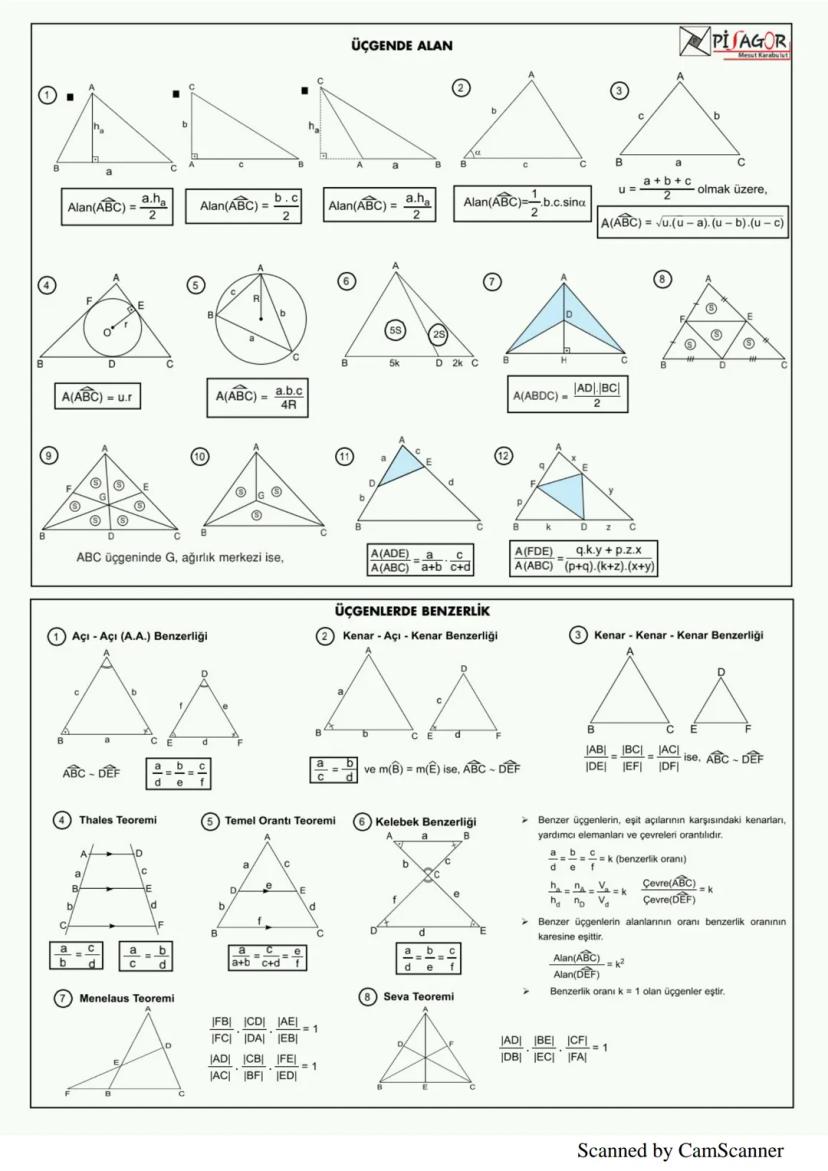
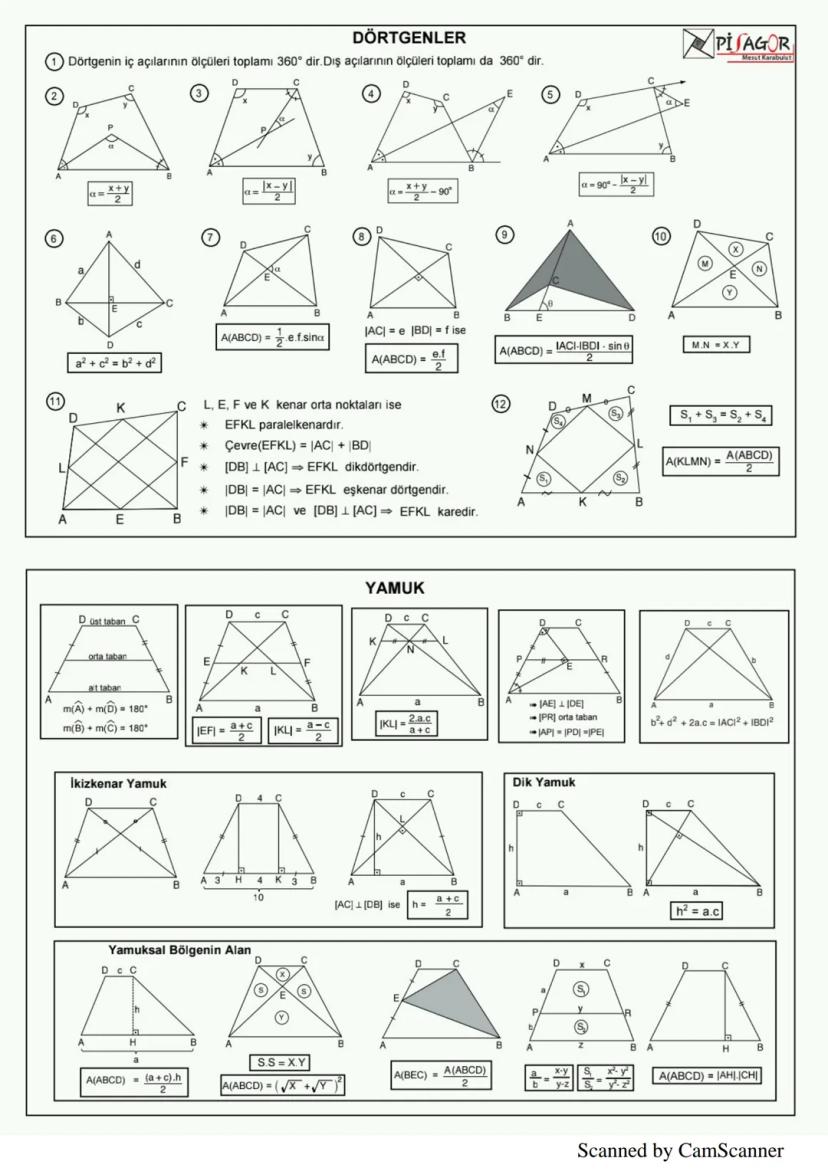
Prizmalar, Piramitler ve Küre

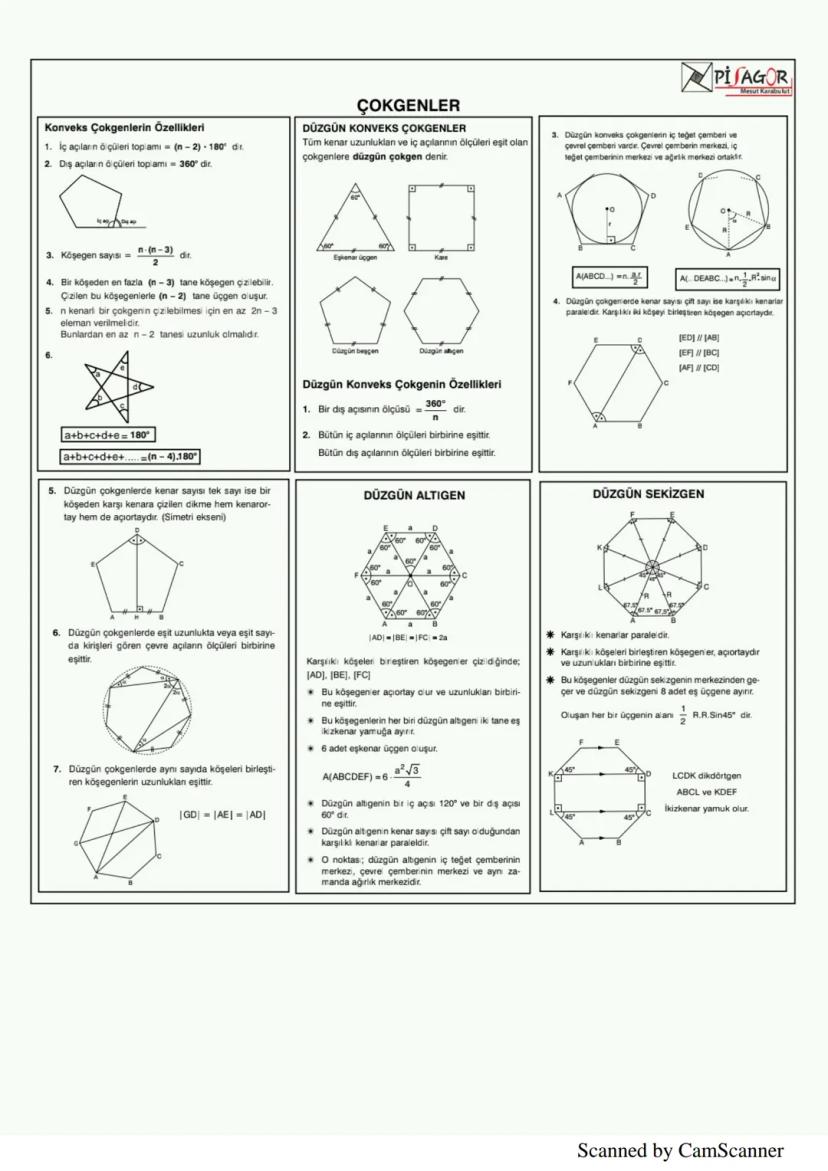
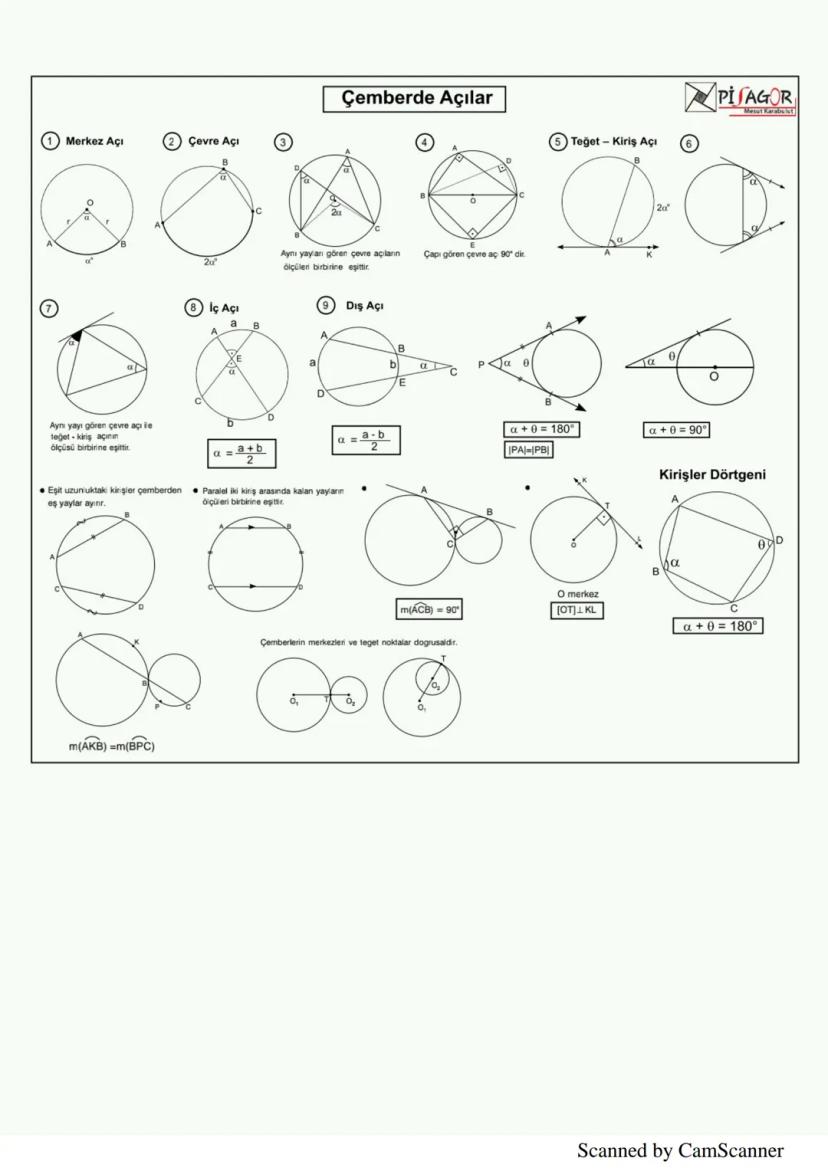
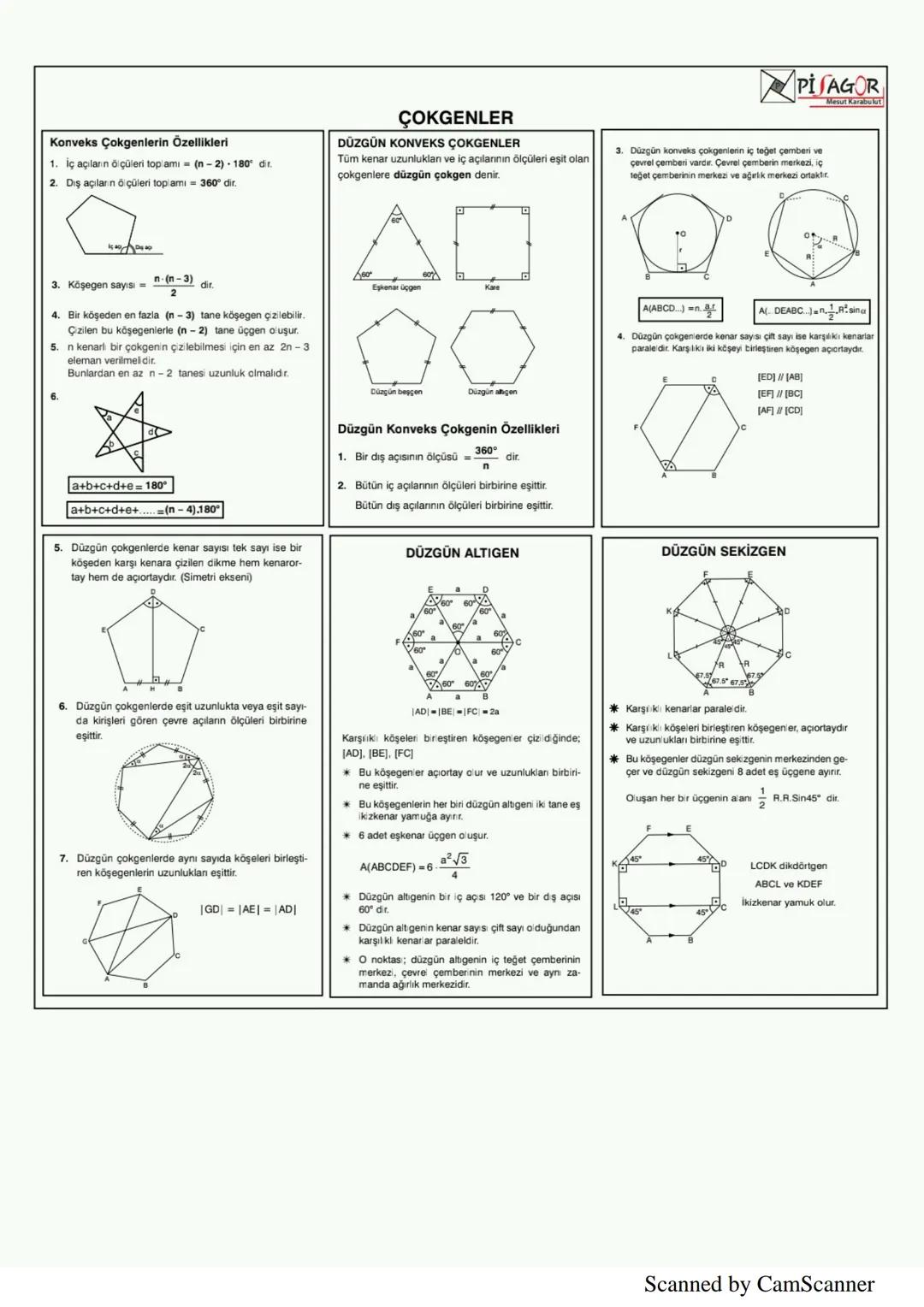
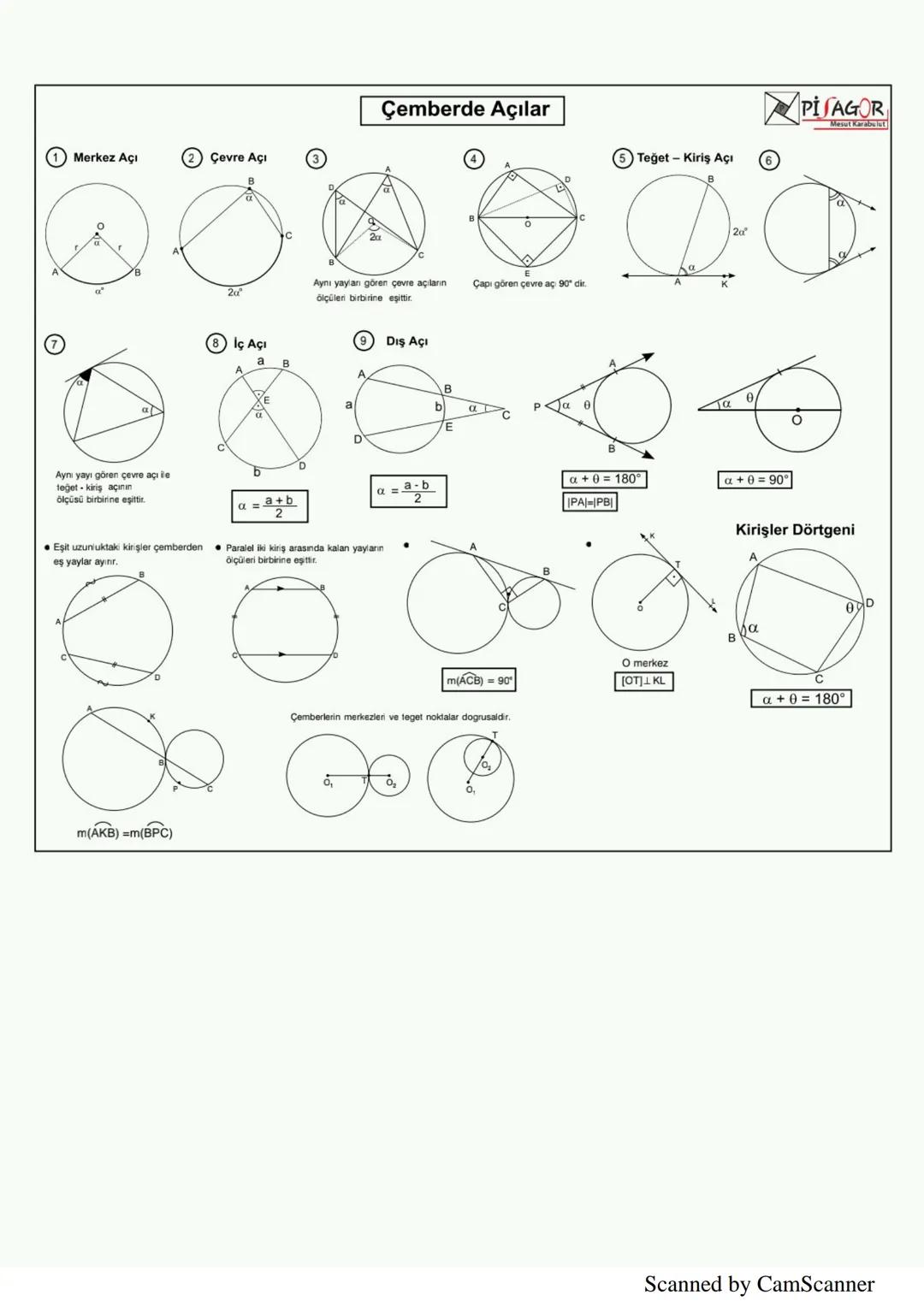
Prizmalar, tabanları eş ve paralel, yanal yüzleri paralelkenar olan üç boyutlu cisimlerdir. Prizmaların yanal alanı taban çevresi × yükseklik, toplam alanı yanal alan + 2 × taban alanı, hacmi ise taban alanı × yükseklik formülüyle hesaplanır.

Dikdörtgenler prizmasının hacmi V = a.b.c formülüyle bulunur. Küpün hacmi V = a³, toplam alanı ise A = 6a²'dir. Silindirin hacmi V = πr²h, yanal alanı 2πrh, toplam alanı ise 2πr$r+h$'dir.

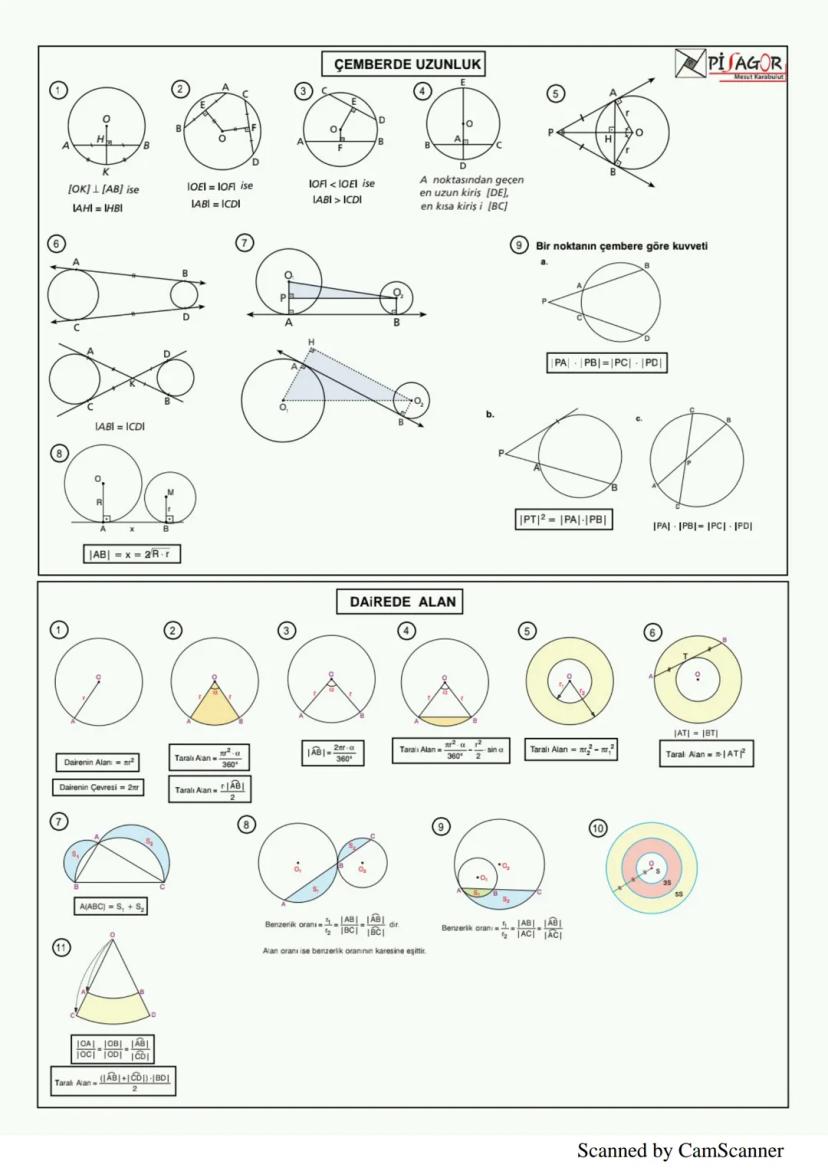
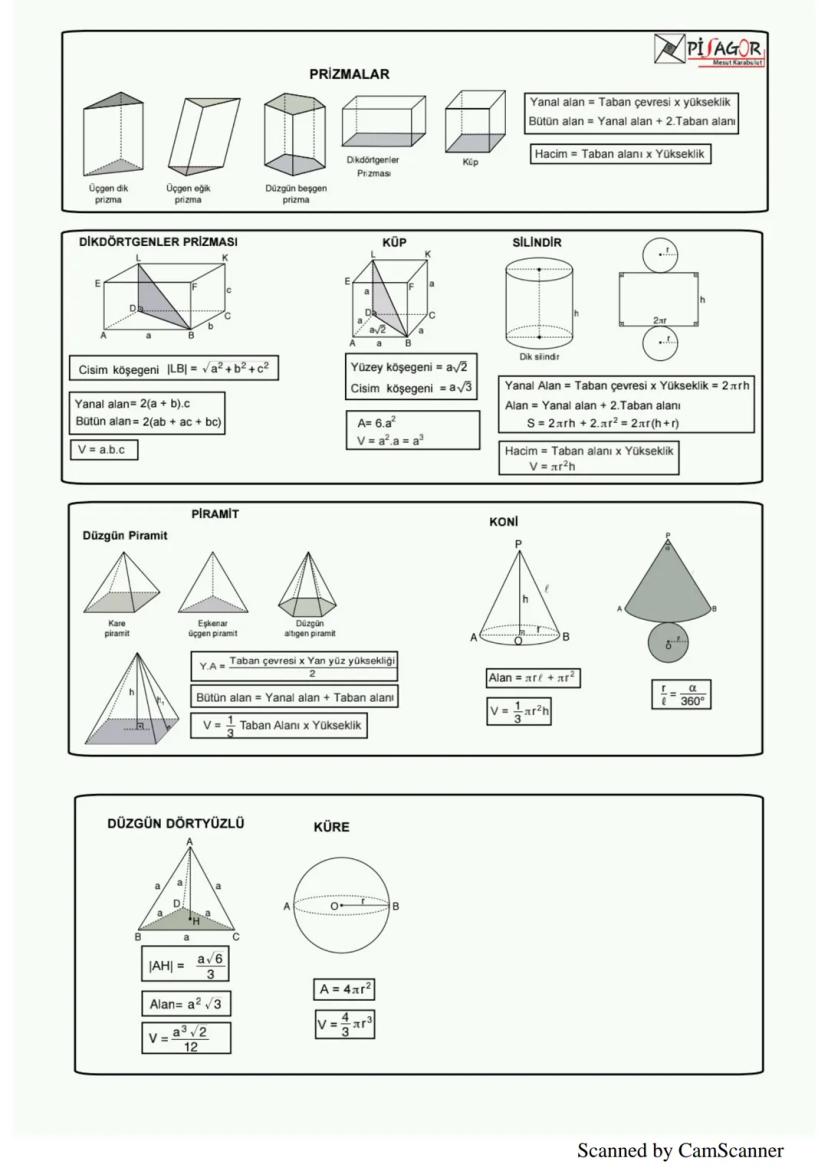
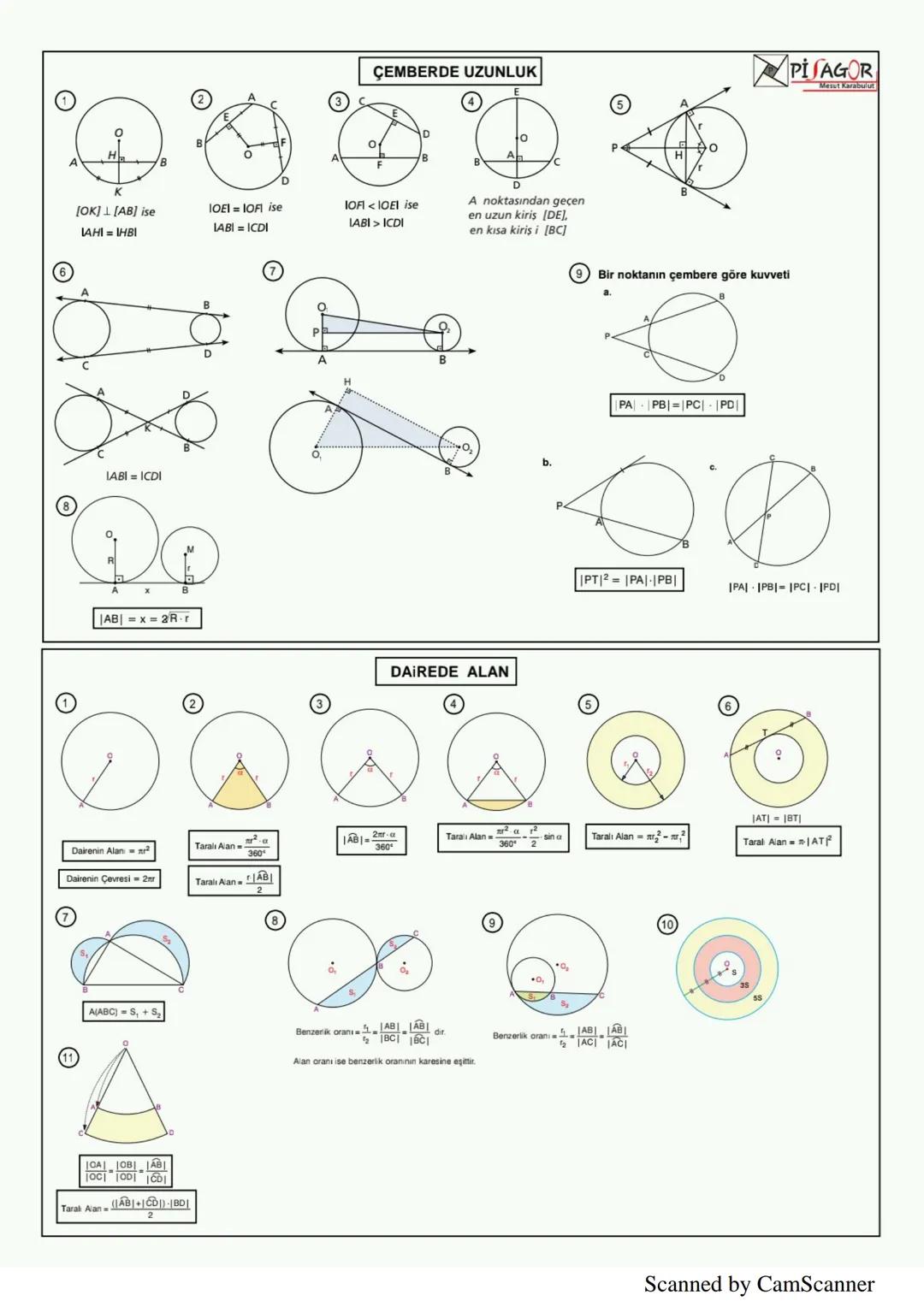
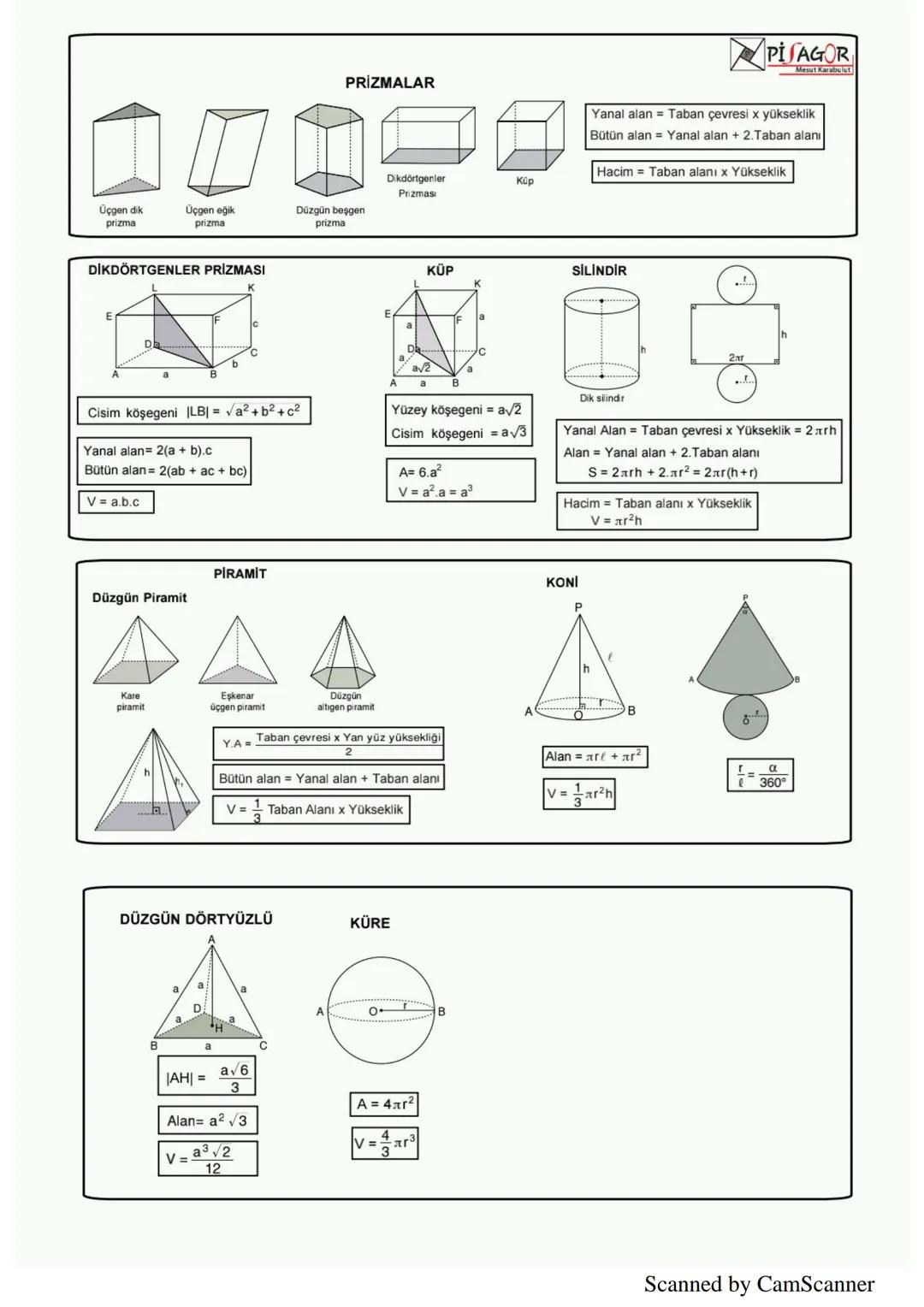
Piramit, bir çokgen taban ve üçgen yanal yüzlerden oluşan cisimdir. Piramidin hacmi V = (taban alanı × yükseklik)/3 formülüyle hesaplanır. Düzgün dörtyüzlünün hacmi V = (a³√2)/12, yüzey alanı ise A = a²√3'tür.

Kürenin hacmi V = (4πr³)/3, yüzey alanı ise A = 4πr² formülleriyle bulunur.

💡 Uzay geometri sorularında, yüzey köşegeni ve cisim köşegeni arasındaki farkı iyi anla. Dikdörtgenler prizmasında cisim köşegeni |DB| = √$a²+b²+c²$ formülüyle bulunur.