Matematik526Güncellendi 2 Eyl 20268 sayfa

9. Sınıf Üçgenler: Temel Açıklamalar ve Sorular

Şikayet Et

𝐥𝐞𝐦𝐨𝐬𝐬@lemoss22

Üçgenlerdeki açı hesaplamalarını öğrenmek sınavlarda sürekli karşılaşacağın önemli bir konu. Bu notlarda hem temel açı kurallarını hem de açıortay, yükseklik gibi özel durumları pratik sorularla göreceğiz.

Ders notlarını görmek için kaydol.
Ücretsiz!

Üçgende Temel Açı Kuralları

Üçgenlerde açı hesaplamalarının temeli iç açılar toplamının 180° olması kuralına dayanıyor. Bu basit kuralı kullanarak karmaşık görünen soruları kolayca çözebilirsin.

İlk soruda EDC üçgeninden başlayıp eksik açıyı buluyoruz: 53° + 74° + x = 180° olduğundan x = 53°. Sonra ABC üçgeninde α + 65° + 53° = 180° yazıp α = 62° buluyoruz.

Dış açılar konusunda unutma ki dış açıların toplamı 360°'dir. İkinci soruda bu kuralı kullanarak $2x+5$ + $x-2$ + 135 = 360 denklemini kuruyoruz ve x = 74° buluyoruz.

Pratik İpucu: Dış açı hesaplamalarında önce iç açıdan dış açıya geçmeyi unutma (180° - iç açı = dış açı).

Ters orantı sorularında ise en büyük dış açı en küçük iç açının yanında olur. Oranları kullanarak açıları bulup, en küçüğün yanındaki dış açıyı hesaplayabilirsin.

Ders notlarını görmek için kaydol.
Ücretsiz!

Dış Açı Kuralı ve Pratik Uygulamalar

Dış açı kuralı geometrinin en kullanışlı formüllerinden biri: "Bir üçgende dış açı, kendisine komşu olmayan iki iç açının toplamına eşittir." Bu kuralı ezberlemen gereken temel bilgilerden.

Dördüncü soruda bu kuralı direkt kullanarak m(EBD) = x + y buluyoruz. Sonra BDE üçgeninin iç açıları toplamından $x+y$ + 2x + 2y = 180° yazıp x + y = 60° sonucuna ulaşıyoruz.

Beşinci soru biraz daha karmaşık görünse de aynı mantıkla çözülüyor. Bumerang kuralını da öğrenmen gerekiyor: α = x + y + z şeklindeki formül.

Dikkat Et: Açı eşitlikleri verildiğinde bu eşitlikleri kullanarak bilinmeyen açıları adım adım bulabilirsin.

Altıncı soruda bumerang kuralını görüyoruz: 76° + x + 36° = 136° olduğundan x = 24°. Bu tür sorularda şekli doğru okumak çok önemli.

Ders notlarını görmek için kaydol.
Ücretsiz!

Açıortay Formülleri ve İç Teğet Merkezi

İç açıortayların kesiştiği noktada açıyı bulmak için α = 90° + A/2 formülünü kullanıyoruz. Bu formülü ezberlemen gerekiyor çünkü sınavda çok sık karşılaşırsın.

Yedinci soruda bu formülü doğrudan uygulayarak 6x = 90° + $4x-4°$ /2 denklemini kuruyoruz ve x = 22° buluyoruz. Formülü doğru yazmak çözümün yarısı demek.

Dış açıortaylar için ise α = 90° - A/2 formülünü kullanıyoruz. Dokuzuncu soruda 43° = 90° - A/2 yazıp A = 94° buluyoruz.

Formül Hatırlatması: İç açıortay = 90° + A/2, Dış açıortay = 90° - A/2

Onuncu soru iç teğet merkezi konusunu içeriyor. I noktası hem iç açıortayların kesişim noktası hem de iç teğet çemberinin merkezi. Bu noktadan çizilen doğrular açıortay özelliği taşır.

Ders notlarını görmek için kaydol.
Ücretsiz!

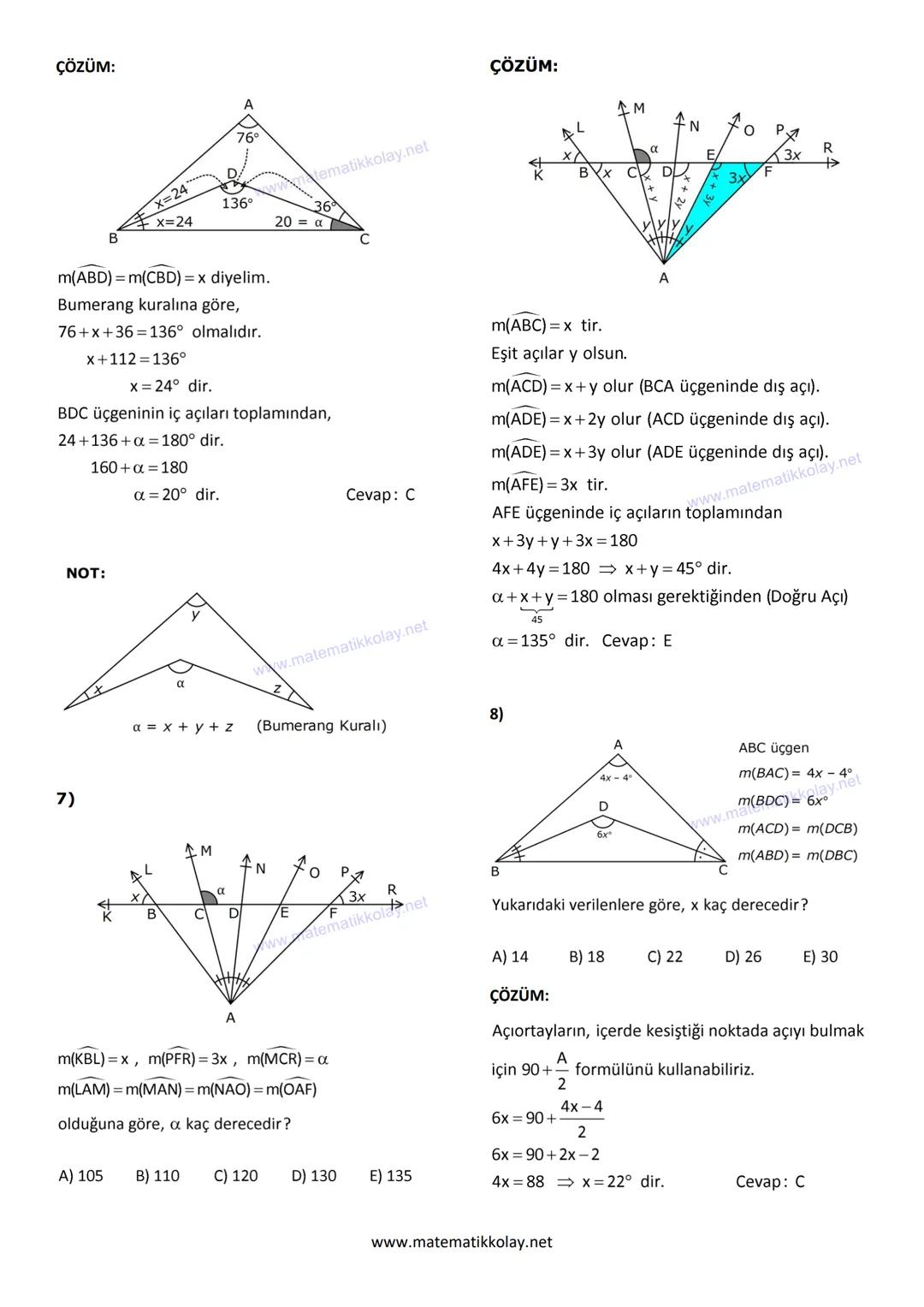
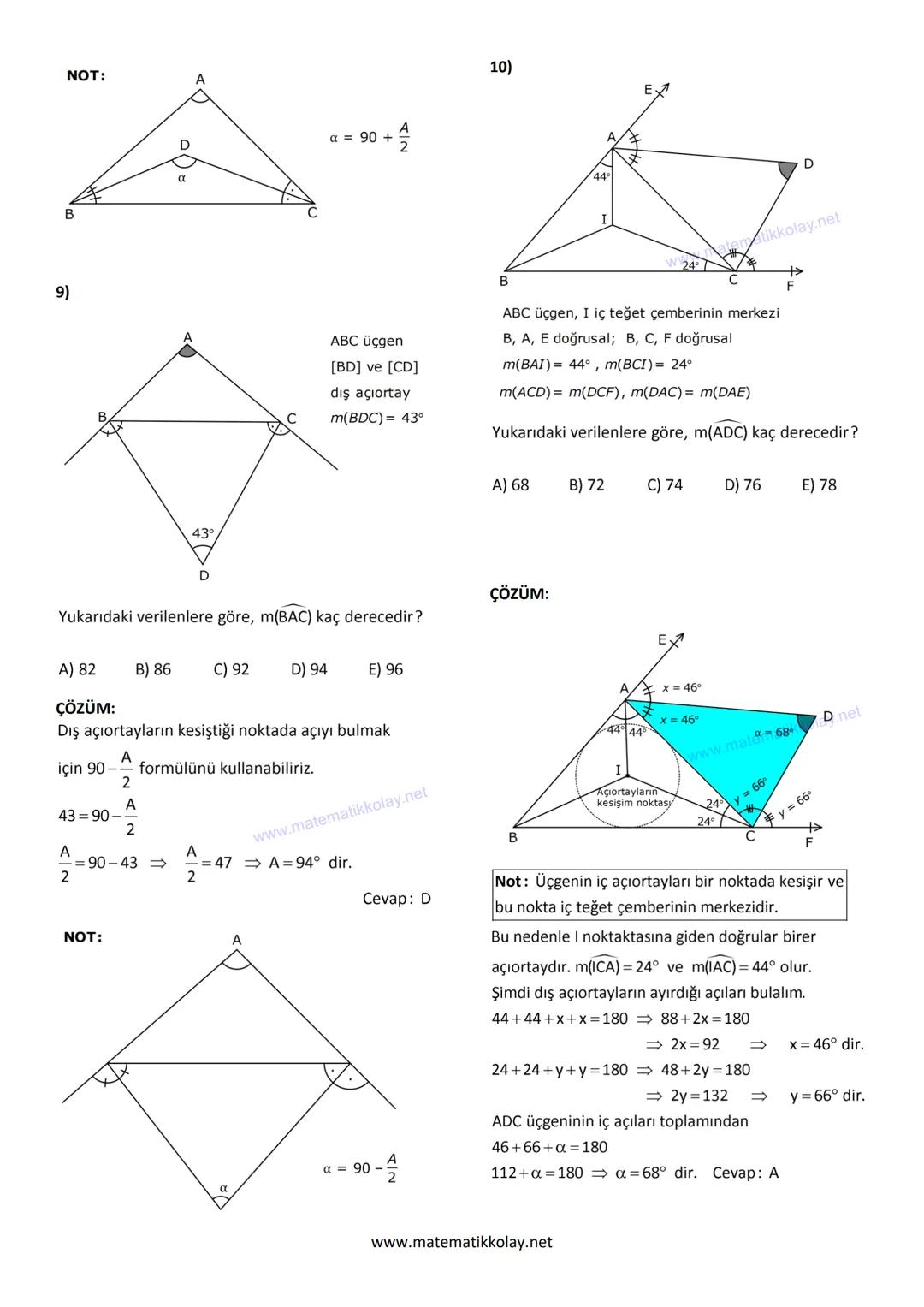
İç ve Dış Açıortay Kesişimleri

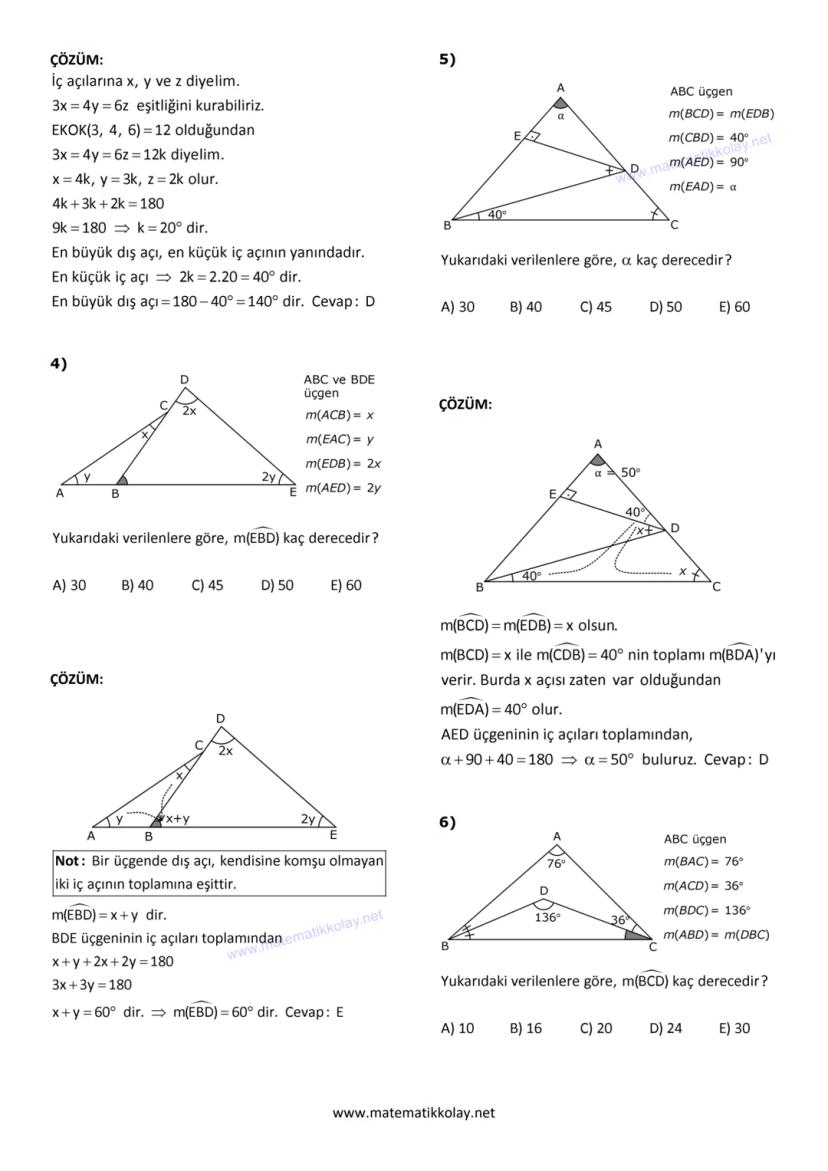
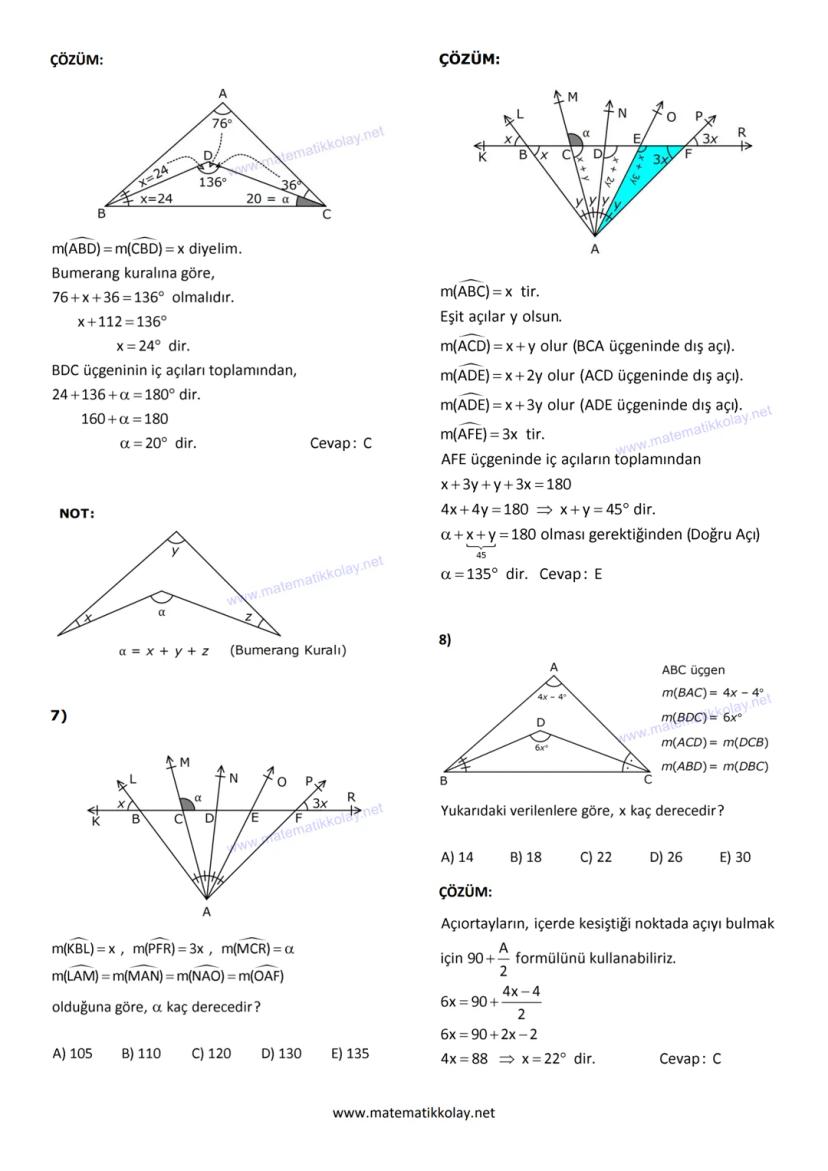
İç açıortay ile dış açıortayın kesişiminde oluşan açı için A/2 formülünü kullanıyoruz. On birinci soruda x + 4 = $3x-24$ /2 denklemini kurarak x = 32° buluyoruz.

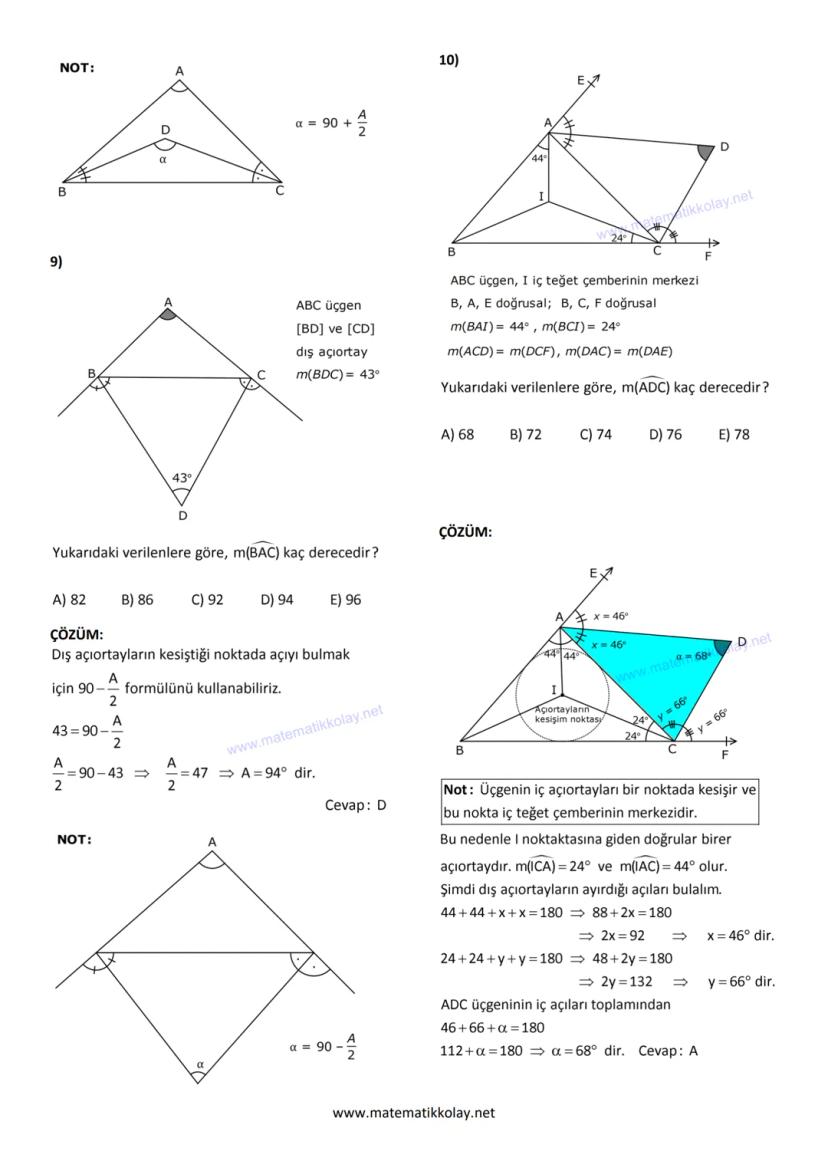
İç teğet merkezi sorularında dikkat etmen gereken nokta, I noktasından çizilen doğruların açıortay özelliği taşıması. Açıortay oldukları için açıları eşit parçalara bölerler.

Onuncu sorunun detayında, önce açıortayların ayırdığı açıları buluyoruz: 44° + 44° + 2x = 180° dan x = 46°, benzer şekilde y = 66°. Sonra ADC üçgeninde 46° + 66° + α = 180° dan α = 68° buluyoruz.

Püf Noktası: İç teğet merkezi sorularında önce açıortayların oluşturduğu eşit açıları belirle, sonra üçgen kurallarını uygula.

Bu tür sorularda sistemli ilerlemek çok önemli. Önce verilen bilgileri kullanarak bilinmeyen açıları bul, sonra üçgen kurallarıyla devam et.

Ders notlarını görmek için kaydol.
Ücretsiz!

İkizkenar Üçgen Özellikleri

İkizkenar üçgenlerde eşit kenarların karşısındaki açılar eşittir. Bu temel özelliği kullanarak birçok soruyu çözebilirsin.

On üçüncü soruda ABC üçgeni ikizkenar olduğundan m(ABC) = α, ABD üçgeni de ikizkenar olduğundan m(ADB) = α. Üç açının toplamı 180° olduğundan 3α = 126°, yani α = 42°.

On dördüncü soruda ise ikizkenar üçgenin taban açılarını buluyoruz: $180° - 80°$ /2 = 50°. Sonra ADC ikizkenar üçgeninde açıları eşit olduğundan hesaplamaları yapıyoruz.

İkizkenar Üçgen Kuralı: Eşit kenarların karşısındaki açılar her zaman eşittir, bu özelliği kullanarak bilinmeyen açıları bulabilirsin.

On beşinci soru daha karmaşık bir ikizkenar üçgen kombinasyonu içeriyor. Burada birden fazla ikizkenar üçgen özelliğini birlikte kullanman gerekiyor.

Ders notlarını görmek için kaydol.
Ücretsiz!

İkizkenar Üçgen ve Özel Durumlar

Karmaşık ikizkenar üçgen sorularında sistemli yaklaşım şart. On beşinci sorunun devamında x = y eşitliğini kullanarak 5x = 190°, dolayısıyla x = 38° buluyoruz.

İkizkenar üçgenin özel özelliği: Tabana inen yükseklik aynı zamanda hem kenarortay hem de açıortaydır. Bu üç özellikten herhangi ikisi varsa üçüncüsü de vardır.

On altıncı soruda bu özelliği kullanıyoruz. DE hem yükseklik hem de kenarortay olduğundan BDC ikizkenar üçgen, yani BD = DC. Bu durumda taban açıları eşit olur.

Önemli Kural: İkizkenar üçgende yükseklik = kenarortay = açıortay özelliği sorularda çok kullanılır.

Çözümde α açısını bulup, ikizkenar üçgen özelliklerini kullanarak 2α + $54° - α$ = 180° denklemini kuruyoruz ve α = 42° buluyoruz.

Ders notlarını görmek için kaydol.
Ücretsiz!

Eşkenar Üçgen ve Açıortay-Yükseklik İlişkisi

Eşkenar üçgende her açı 60° ve tüm kenarlar eşit. Ayrıca yükseklik, kenarortay ve açıortay aynı doğru üzerinde bulunur.

On yedinci soruda AEC ikizkenar üçgen oluyor çünkü AE = AB = AC. m(ACE) = 70° olduğundan m(AEC) = 70°, geriye kalan m(EAC) = 40°. Sonunda m(BAE) = 60° - 40° = 20°.

On sekizinci soruda eşkenar üçgenin özelliklerini kullanıyoruz. BD hem açıortay hem yükseklik olduğundan 60°'yi ikiye böler ve BDC'de 90° açı oluşturur.

Eşkenar Üçgen Kuralı: Yükseklik, kenarortay ve açıortay özellikleri aynı doğruda birleşir.

Açıortay ile yükseklik arasındaki açı için |B - C|/2 formülü var. On dokuzuncu soruda |44° - 68°|/2 = 12° buluyoruz.

Ders notlarını görmek için kaydol.
Ücretsiz!

Hiç sormayacaksın sanmıştık...

Yapay zeka arkadaşımız öğrencilerin ihtiyaçlarına göre özel olarak tasarlanmıştır. Platformda bulunan milyonlarca içeriğe dayanarak öğrencilere gerçekten anlamlı ve ilgili yanıtlar verebiliyoruz. Ancak mesele sadece cevaplar değil, refakatçi aynı zamanda kişiselleştirilmiş öğrenme planları, sınavlar veya sohbet içerikleri ve öğrencilerin becerilerine ve gelişimlerine dayalı %100 kişiselleştirme ile öğrencilere günlük öğrenme zorluklarında rehberlik ediyor.

Uygulamayı Google Play Store ve Apple App Store'dan indirebilirsiniz.

Knowunity uygulaması ücretsiz! Uygulamamız çok yakında indirmeye hazır olacak, bekle bizi. 💙

9. Sınıf Üçgenler: Temel Açıklamalar ve Sorular

Üçgende Temel Açı Kuralları

Dış Açı Kuralı ve Pratik Uygulamalar

Açıortay Formülleri ve İç Teğet Merkezi

İç ve Dış Açıortay Kesişimleri

İkizkenar Üçgen Özellikleri

İkizkenar Üçgen ve Özel Durumlar

Eşkenar Üçgen ve Açıortay-Yükseklik İlişkisi

Hiç sormayacaksın sanmıştık...

Knowunity yapay zeka arkadaşı nedir?

Knowunity uygulamasını nereden indirebilirim?

Knowunity ücretsiz mi?

Benzer Ders Notları

7. Sınıf Doğrular ve Açı

GEOMETRİ DOĞRUDA AÇILAR

Matematik açılar PDF test

Matematik

Trigonometri

DOĞRUDA ACILAR

En popüler içerikler: Angle

GEOMETRİ DOĞRUDA AÇILAR

DOĞRUDA ACILAR

5 sınıf matematik açılar ile ilgili sorular

En popüler içerikler: Matematik

8.sınıf matematik

8. Sınıf matematik ders notları

Tyt matematik

8. Sınıf LGS Matematik Çarpanlar ve Katlar Konu Anlatımı

TYT matematik ders notları

10 Günde Temel Atma Garanti TYT Matematik

EBOB&EKOK

MED Koçluk AYT Matematik Notları

LGS MATEMATİK NOTLARI

En popüler içerikler

Tyt biyoloji

8.sınıf matematik

8. Sınıf matematik ders notları

9. Sınıf Tarih Konu Anlatımı

TYT AYT TARİH

TYT Fizik

Tyt kimya konu başlıkları

TYT Fizik

Tyt matematik

Kullanıcılarımızdan yorumlar. Onlar her şeyi çok beğendi, sen de beğeneceksin.