Trigonometri

Trigonometri, dik üçgenlerle başlayıp çemberlere ve açılara uzanan matematikteki önemli bir alandır. Birim çember matematikteki harika bir araçtır - merkezi orijinde ve yarıçapı 1 birim olan çemberdir.

Birim çemberde, bir nokta A(x,y) ise, bu noktanın koordinatları trigonometrik değerlere bağlıdır:

• sinüs değeri = y koordinatı
• kosinüs değeri = x koordinatı
• tanjant değeri = y/x $sinüs/kosinüs$

Trigonometrik fonksiyonlar, bölgelere göre farklı işaretlere sahiptir:

• 1. bölgede: sin > 0, cos > 0
• 2. bölgede: sin > 0, cos < 0
• 3. bölgede: sin < 0, cos < 0
• 4. bölgede: sin < 0, cos > 0

Hatırlaman gereken temel formül: sin²α + cos²α = 1 formülü trigonometride çok işine yarayacak!

Ayrıca, Sinüs Teoremi ve Kosinüs Teoremi üçgenlerde açılar ve kenarlar arasındaki ilişkileri bulmamızı sağlar. Bu teoremler özellikle dik olmayan üçgenlerle çalışırken çok kullanışlıdır.

Analitik Geometri

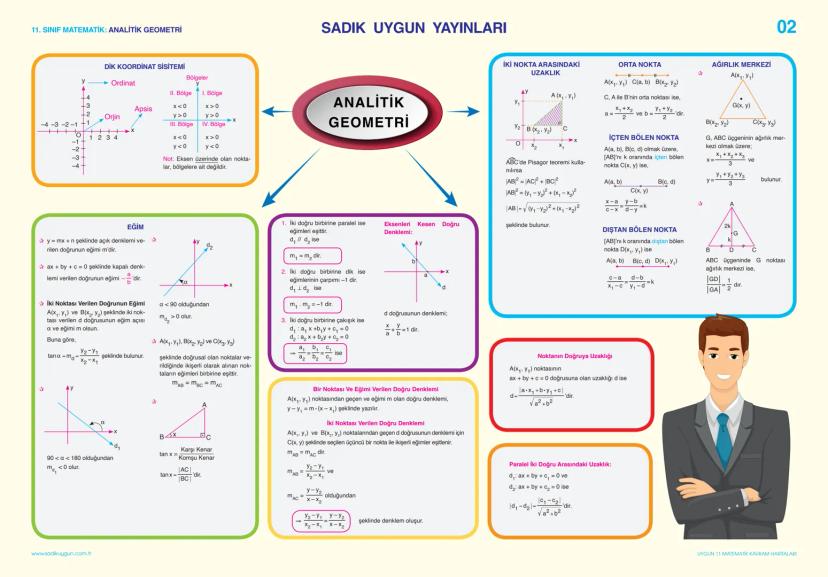
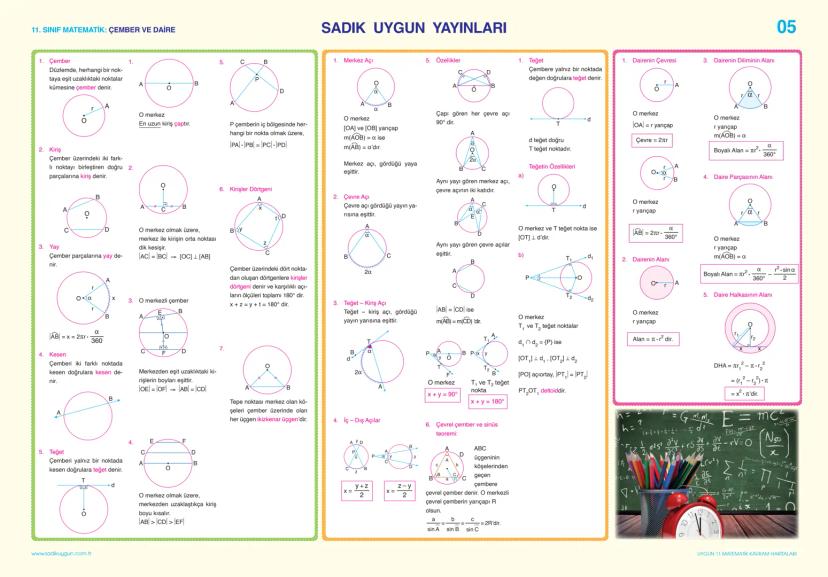
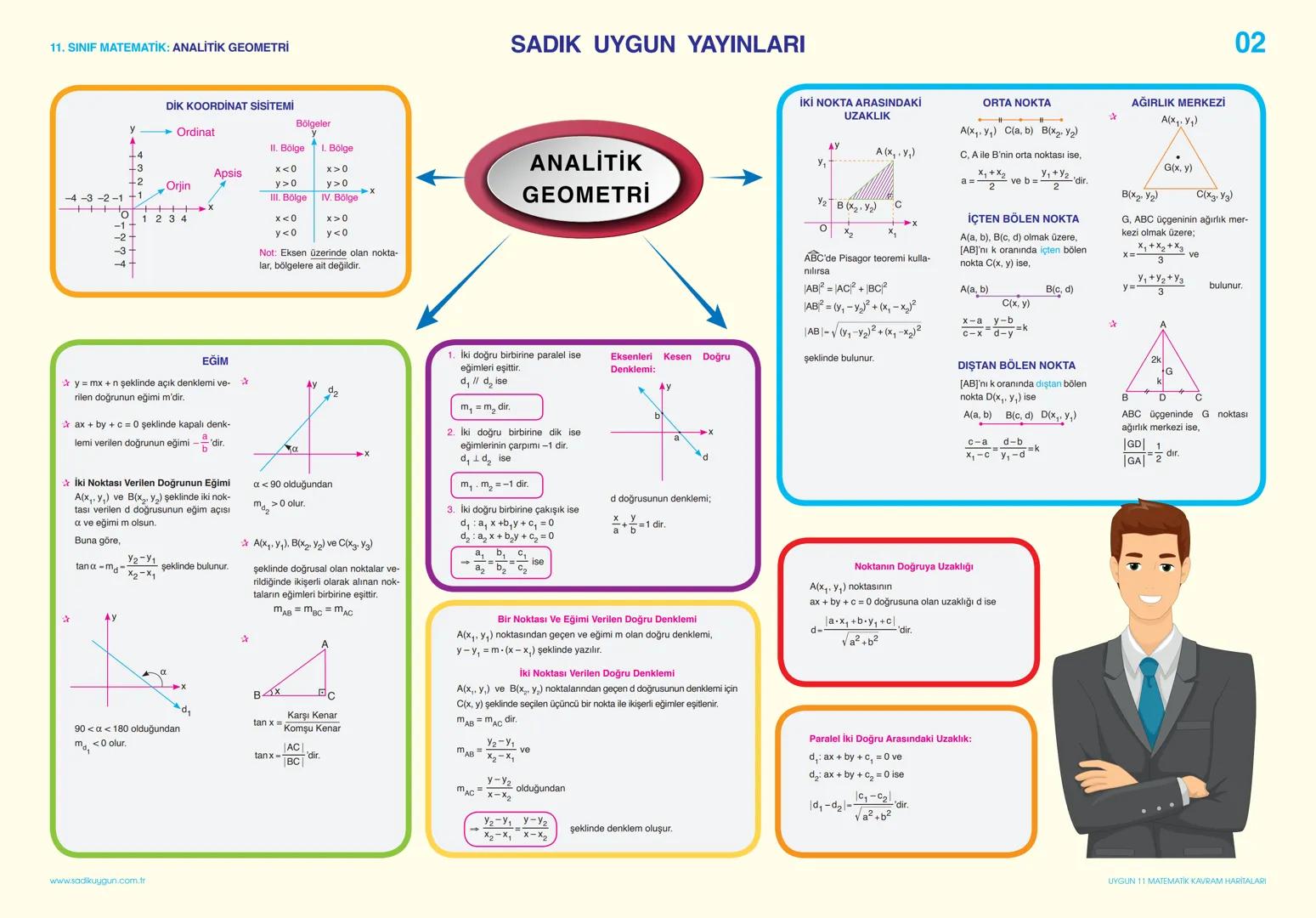
Analitik geometri, koordinat sisteminde şekilleri incelemenin harika bir yoludur. Önce dik koordinat sistemini tanıyalım: Düzlemi dört bölgeye ayıran x ve y eksenleriyle oluşur.

İki nokta A(x₁, y₁) ve B(x₂, y₂) verildiğinde:

• Aralarındaki uzaklık: d = √$(x₂-x₁)² + (y₂-y₁)²$
• Orta noktası: M$(x₁+x₂)/2, (y₁+y₂)/2$

Doğrular, analitik geometrinin temel elemanlarıdır ve eğim kavramı çok önemlidir. Eğim (m), bir doğrunun yatay eksenle yaptığı açının tanjantıdır. İki nokta arasındaki eğim formülü:

m = $y₂-y₁$/$x₂-x₁$

Bir doğruya ait özellikler:

• İki doğru paralel ise eğimleri eşittir $m₁ = m₂$
• İki doğru dik ise eğimlerinin çarpımı -1'dir $m₁ × m₂ = -1$

Matematikteki harika şey: Bir noktanın doğruya uzaklığını hesaplamak için d = |ax₁+by₁+c|/√$a²+b²$ formülünü kullanabilirsin!

Analitik geometri, geometri problemlerini cebirsel yöntemlerle çözmeye olanak tanır. Bu sayede karmaşık geometrik şekiller ve uzaklıklar kolayca hesaplanabilir.

Fonksiyonlarda Uygulamalar

Fonksiyonların gerçek hayatta pek çok uygulaması vardır. Bir fonksiyonun davranışını anlamak için artma-azalma durumlarını, maksimum-minimum noktalarını incelemek çok önemlidir.

Bir fonksiyonun artması, x değeri arttıkça f(x) değerinin de artması demektir. Azalması ise tam tersidir. Ayrıca fonksiyonlar tek veya çift olabilir:

• Çift fonksiyonlar için f$-x$ = f(x) geçerlidir ve grafikleri y eksenine göre simetriktir
• Tek fonksiyonlar için f$-x$ = -f(x) geçerlidir ve grafikleri orijine göre simetriktir

Paraboller (ikinci dereceden fonksiyonlar) özel fonksiyonlardır. f(x) = ax² + bx + c biçimindeki bir parabolün:

• Eğer a > 0 ise kolları yukarı, a < 0 ise kolları aşağı bakar
• Tepe noktası r = -b/2a formülüyle bulunur
• Tepe noktasında fonksiyon maksimum veya minimum değerini alır

Bunu bilmek işine yarayacak: Bir fonksiyonu grafiğe çizerken önce kesişim noktalarını, sonra tepe noktasını bulursan işin çok daha kolay olur!

Fonksiyonların dönüşümleri de çok kullanışlıdır. f(x) grafiğini yukarı, aşağı, sağa veya sola öteleyerek yeni fonksiyon grafikleri oluşturabilirsin.

Denklem ve Eşitsizlik Sistemleri

İkinci dereceden denklem sistemleri, matematikteki önemli konulardan biridir. Genel formülü: ax² + by² + cxy + dx + ey + f = 0 şeklindedir. Bu sistemlerin çözümü, iki eğrinin kesişim noktalarını bulmak anlamına gelir.

İkinci dereceden eşitsizlikler $ax² + bx + c > 0, ax² + bx + c < 0 gibi$ grafik yöntemi kullanılarak çözülebilir:

1. Önce denklemi çöz $ax² + bx + c = 0$
2. Bulduğun kökler sayı doğrusunu parçalara ayırır
3. Her aralıkta eşitsizliğin işaretini kontrol et

Pratik bir ipucu: İkinci dereceden eşitsizlikleri çözerken, bir test noktası seçip eşitsizliğin işaretinin doğru olup olmadığını kontrol etmek işini çok kolaylaştırır!

Eşitsizlik sistemlerinde, her bir eşitsizliğin çözüm kümesini bulup, bu kümelerin kesişimini almak gerekir. Bu işlem genellikle koordinat düzleminde bölgeleri tarayarak yapılır.

Denklem ve eşitsizlik sistemleri gerçek hayat problemlerinin modellenmesinde sıkça kullanılır. Özellikle ekonomi, mühendislik ve bilimsel hesaplamalarda bu sistemler karşımıza çıkar.

Çember ve Daire

Çember, düzlemde bir noktaya (merkez) eşit uzaklıktaki noktalar kümesidir. Çemberle ilgili temel kavramlar:

• Kiriş: Çember üzerindeki iki noktayı birleştiren doğru parçası
• Yay: Çember parçaları
• Teğet: Çemberi yalnızca bir noktada kesen doğru

Çemberde açılar çok önemlidir:

• Merkez açı: Tepe noktası çemberin merkezinde olan açı
• Çevre açı: Tepe noktası çember üzerinde olan açı
• Bir çemberde, aynı yayı gören merkez açı, çevre açının iki katıdır
• Çapı gören her çevre açı 90°'dir

Dairenin alanı ve çevresi için temel formüller:

• Çevre = 2πr
• Alan = πr²
• Daire dilimi alanı = πr² × (α/360°) (α merkez açı ölçüsü)

Sınavda işine yarayacak bilgi: Çember üzerindeki dört noktadan oluşan dörtgenlere kirişler dörtgeni denir ve karşılıklı açılarının toplamı 180° olur!

Teğet-kiriş açı, gördüğü yayın yarısına eşittir. Ayrıca, bir çembere dışarıdan çizilen iki teğet doğrunun, teğet noktalarını birleştiren doğrulara eşit uzaklıktadır.

Olasılık

Olasılık, belirsiz durumların matematiksel olarak incelenmesidir. Temel kavramlar:

• Deney: Para atılması, zar atılması gibi sonucu belirsiz işlemler
• Örnek Uzay (E): Bir deneyde olası tüm sonuçların kümesi
• Olay: Örnek uzayın herhangi bir alt kümesi

Olasılık hesaplarında temel formül: P(A) = İstenen durumların sayısı / Olası tüm durumların sayısı

Olasılık kuralları:

• 0 ≤ P(A) ≤ 1 (Olasılık değeri 0 ile 1 arasındadır)
• P(E) = 1 (Kesin olayın olasılığı 1'dir)
• P(A) + P(A') = 1 (Bir olayın ve tersinin olasılıkları toplamı 1'dir)

Bağımsız olaylar, birinin gerçekleşmesinin diğerinin olasılığını etkilemediği olaylardır. A ve B bağımsız olaylarsa: P(A∩B) = P(A) × P(B)

Koşullu olasılık, B olayı gerçekleştiğinde A olayının gerçekleşme olasılığıdır: P(A|B) = P(A∩B) / P(B)

Bir püf nokta: Para ve zar atma gibi deneylerde, atış sayısı arttıkça olası sonuçların sayısı katlanarak artar (n para için 2ⁿ, n zar için 6ⁿ)!

İki tür olasılık vardır: Deneysel olasılık (denemeler yaparak hesaplanan) ve Teorik olasılık (matematiksel olarak hesaplanan).