Geometrik Şekiller: Dik Üçgende Trigonometrik Oranlar

Trigonometri, dik üçgenlerdeki açı ve kenar uzunlukları arasındaki ilişkiyi incelememize yardımcı olur. Bu konuyu öğrenmek, hem geometri problemlerini çözmede hem de gerçek hayatta karşılaştığımız birçok durumu analiz etmede çok işimize yarayacak.

10. sınıf matematik dersinde göreceğimiz bu konuda, dik üçgenlerde sinüs, kosinüs, tanjant ve kotanjant olmak üzere dört temel trigonometrik oran öğreneceğiz. Bu oranlar, üçgenlerin kenarları arasındaki ilişkiden türetilir ve her biri bir açıyla ilişkilidir.

Konuyu anlamak için dik üçgendeki kenarların isimlerini bilmek önemli: hipotenüs (dik açının karşısındaki kenar), karşı dik kenar ve komşu dik kenar. Bu kenarlar arasındaki oranlar, açıların trigonometrik değerlerini oluşturur.

💡 Hatırlatma: Dik üçgendeki açıların toplamı her zaman 180 derecedir ve bunlardan biri 90 derecedir. Bu yüzden diğer iki açı toplamı 90 derece olup, bunlar "dar açı" olarak adlandırılır.

Dik Üçgenlerde Trigonometrik Oranların Tanımları

Dik bir üçgende a açısının trigonometrik oranlarını düşünelim. Bu oranlar dik üçgenin kenarları arasındaki ilişkiyi gösterir ve birçok problemi çözmede bize yardımcı olur.

Sinüs (sina): Karşı dik kenar uzunluğunun hipotenüs uzunluğuna oranıdır. sina = (Karşı dik kenar) / (Hipotenüs)

Kosinüs (cosa): Komşu dik kenar uzunluğunun hipotenüs uzunluğuna oranıdır. cosa = (Komşu dik kenar) / (Hipotenüs)

Tanjant (tana): Karşı dik kenar uzunluğunun komşu dik kenar uzunluğuna oranıdır. Aynı zamanda sinüs değerinin kosinüs değerine oranı olarak da bulunabilir. tana = (Karşı dik kenar) / (Komşu dik kenar) = sina / cosa

Kotanjant (cota): Komşu dik kenar uzunluğunun karşı dik kenar uzunluğuna oranıdır. Tanjantın tersi olarak da düşünülebilir. cota = (Komşu dik kenar) / (Karşı dik kenar) = 1 / tana

💡 İpucu: Trigonometrik oranları hatırlamanın kolay bir yolu: Sinüs karşıda, kosinüs komşuda, tanjant ise ikisinin bölümüdür!

Trigonometrik Oranların Uygulamaları

Trigonometrik oranlar, çeşitli geometrik problemleri çözmede oldukça kullanışlıdır. Bu oranlar arasında bazı önemli ilişkiler vardır ve bunlar problemleri çözerken işimizi kolaylaştırır.

Dik üçgenlerde benzerlik özelliği sayesinde, eşit açılara sahip üçgenlerin trigonometrik oranları da aynıdır. Örneğin, farklı boyutlarda iki dik üçgende aynı açının sinüs değerleri birbirine eşittir. Bu özellik sayesinde, bir açının trigonometrik değerini biliyorsak, o açıyı içeren herhangi bir dik üçgende aynı trigonometrik değeri kullanabiliriz.

Bazen bir trigonometrik oran verildiğinde, diğer oranları bulmamız gerekebilir. Örneğin, sina değeri verildiğinde, cosa, tana ve cota değerlerini bulabilmek için bir dik üçgen çizebilir ve Pisagor teoremini kullanabiliriz.

Gerçek hayatta da bu oranları kullanırız: Bir çubuğun gölge uzunluğundan yüksekliğini hesaplama, bir binanın yüksekliğini bulma veya yol eğimini belirleme gibi durumlarda trigonometrik oranlar çok işimize yarar.

💡 Önemli Not: Bir dik üçgende, iki dar açı birbirinin tümleyenidir (toplamları 90° eder). Eğer a ve β bu açılarsa, sina = cosβ ve cosa = sinβ ilişkisi her zaman geçerlidir.

Trigonometrik Özdeşlikler

Trigonometrik oranlara dayalı bazı önemli özdeşlikler vardır. Bu özdeşlikler, trigonometri problemlerinde hesaplamaları kolaylaştırır ve çözümlerin daha hızlı bulunmasını sağlar.

En temel trigonometrik özdeşlik sin²a + cos²a = 1 şeklindedir. Bu formül, herhangi bir a açısı için her zaman geçerlidir ve Pisagor teoreminin trigonometrik bir yorumudur. Bu özdeşliği kullanarak, bir açının bir trigonometrik oranını bildiğimizde diğerini kolayca hesaplayabiliriz.

Bir diğer önemli özdeşlik tana × cota = 1 dir. Bu formül de tanjant ve kotanjantın birbirinin tersi olması gerçeğinden gelir. Örneğin, bir açının tanjant değeri 3 ise, kotanjant değeri 1/3'tür.

Bu özdeşlikleri kullanarak çözebileceğimiz problem türleri şunlardır:

• Bir açının bir trigonometrik değeri verildiğinde diğerlerini bulma
• Trigonometrik ifadelerin değerlerini hesaplama
• Geometrik problemlerde açıları ve kenar uzunluklarını belirleme

💡 Pratik İpucu: Bir trigonometrik değeri bildiğinizde, bir dik üçgen çizerek ve Pisagor teoremini kullanarak diğer değerleri hesaplayabilirsiniz. Örneğin, sina = 1/√5 ise, a²+b² = c² formülünden yola çıkarak diğer değerleri bulabilirsiniz.

Trigonometrik Özdeşliklerin Kullanımı

Trigonometrik özdeşlikler, karmaşık görünen birçok problemi basitleştirmemize yardımcı olur. Bu özdeşlikler sayesinde, trigonometrik ifadeleri dönüştürebilir ve hesaplamaları kolaylaştırabiliriz.

Bir dik üçgende sin²a + cos²a = 1 özdeşliği, Pisagor teoreminden türetilmiştir. Bu özdeşliği kullanarak, bir açının sinüs veya kosinüs değerinden diğerini bulabiliriz. Örneğin, cosa = 3/5 ise, sin²a + $3/5$² = 1 denkleminden sina değerini hesaplayabiliriz.

tana × cota = 1 özdeşliği de çok kullanışlıdır. Bu özdeşlik, tanjant ve kotanjantın birbirinin tersi olduğunu gösterir. Ayrıca, tana = sina/cosa ve cota = cosa/sina olduğunu hatırlarsak, tana × cota = (sina × cosa) / (cosa × sina) = 1 olduğunu görebiliriz.

Trigonometrik ifadeleri içeren denklemleri çözerken bu özdeşlikleri kullanmak çözümü çok kolaylaştırır. Örneğin, sina + cosa = 5/4 gibi bir denklemde, sina × cosa değerini bulmak için (sina + cosa)² = sin²a + cos²a + 2sina × cosa formülünü kullanabiliriz.

💡 Problem Çözme Stratejisi: Trigonometrik denklemleri çözerken önce bilinen özdeşlikleri kullanmayı deneyin. Birçok problem, sin²a + cos²a = 1 veya tana × cota = 1 gibi temel özdeşliklerle çözülebilir.

Trigonometrinin Gerçek Hayat Uygulamaları

Trigonometri, sadece matematik kitaplarındaki soyut bir konu değil, günlük hayatımızda karşılaştığımız birçok problemi çözmemize yardımcı olan güçlü bir araçtır. Gerçek dünya uygulamalarıyla trigonometri daha anlamlı hale gelir.

Bir sokak lambasının yüksekliğini veya bir binanın tepesine olan uzaklığı ölçmek istediğimizde trigonometri kullanırız. Örneğin, 4,8 metre yüksekliğindeki bir direğin ucundaki lambanın oluşturduğu açıları hesaplarken sinüs, kosinüs veya tanjant fonksiyonlarından yararlanırız.

Mühendislikte, mimaride ve navigasyonda trigonometri vazgeçilmezdir. Bir evin çatı eğimini hesaplamak, bir köprünün dayanıklılığını test etmek veya bir geminin rotasını belirlemek için trigonometrik fonksiyonlar kullanılır.

Hatta günlük nesneler arasındaki açıları ve mesafeleri hesaplarken de trigonometriden faydalanırız. Şekil 2'deki gibi eğik duran iki kalemin oluşturduğu açıyı bulurken veya bir bariyerin açılma miktarını hesaplarken tanjant, kotanjant gibi oranları kullanırız.

💡 Bunu Biliyormuydunuz? GPS sistemleri, konumunuzu belirlerken trigonometrik hesaplamalar kullanır. Uydulardan gelen sinyallerin üçgenleme yöntemiyle işlenmesi, yeryüzündeki kesin konumunuzu tespit etmeyi sağlar.

Problem Çözme Stratejileri

Trigonometri problemlerini çözmek başlangıçta zor görünebilir, ama doğru stratejilerle bu zorlukların üstesinden gelebilirsin. İşte trigonometri problemlerini çözmeni kolaylaştıracak bazı ipuçları!

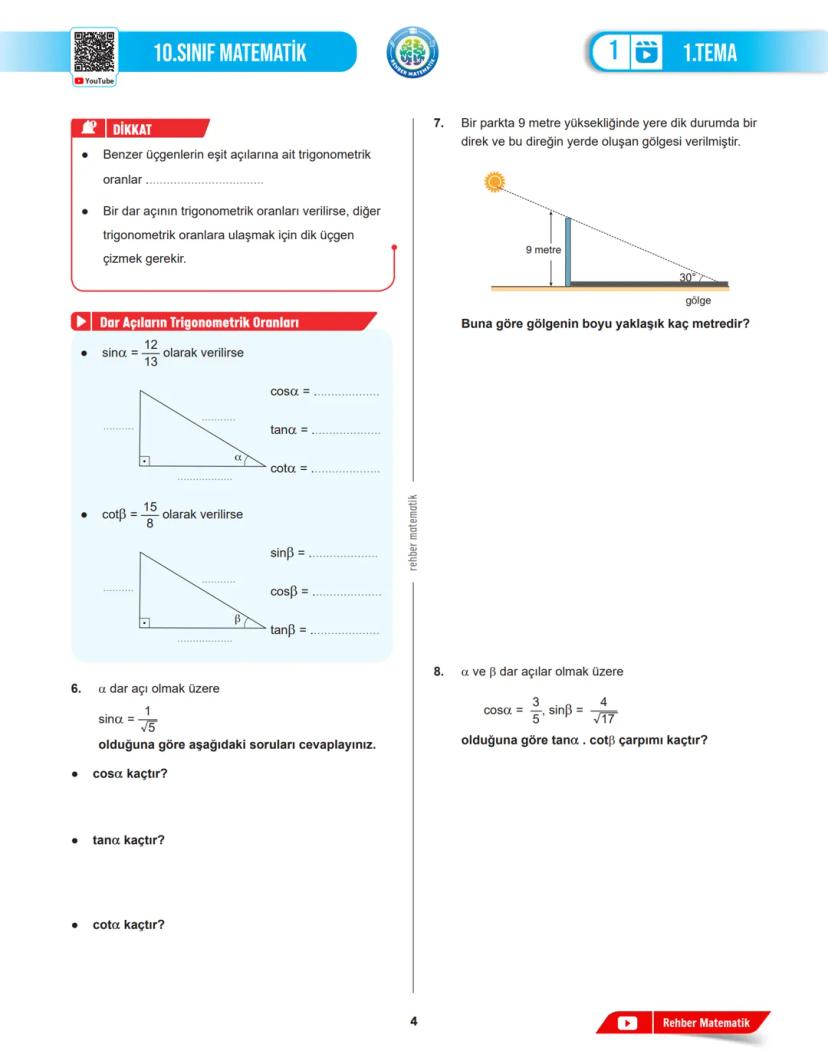
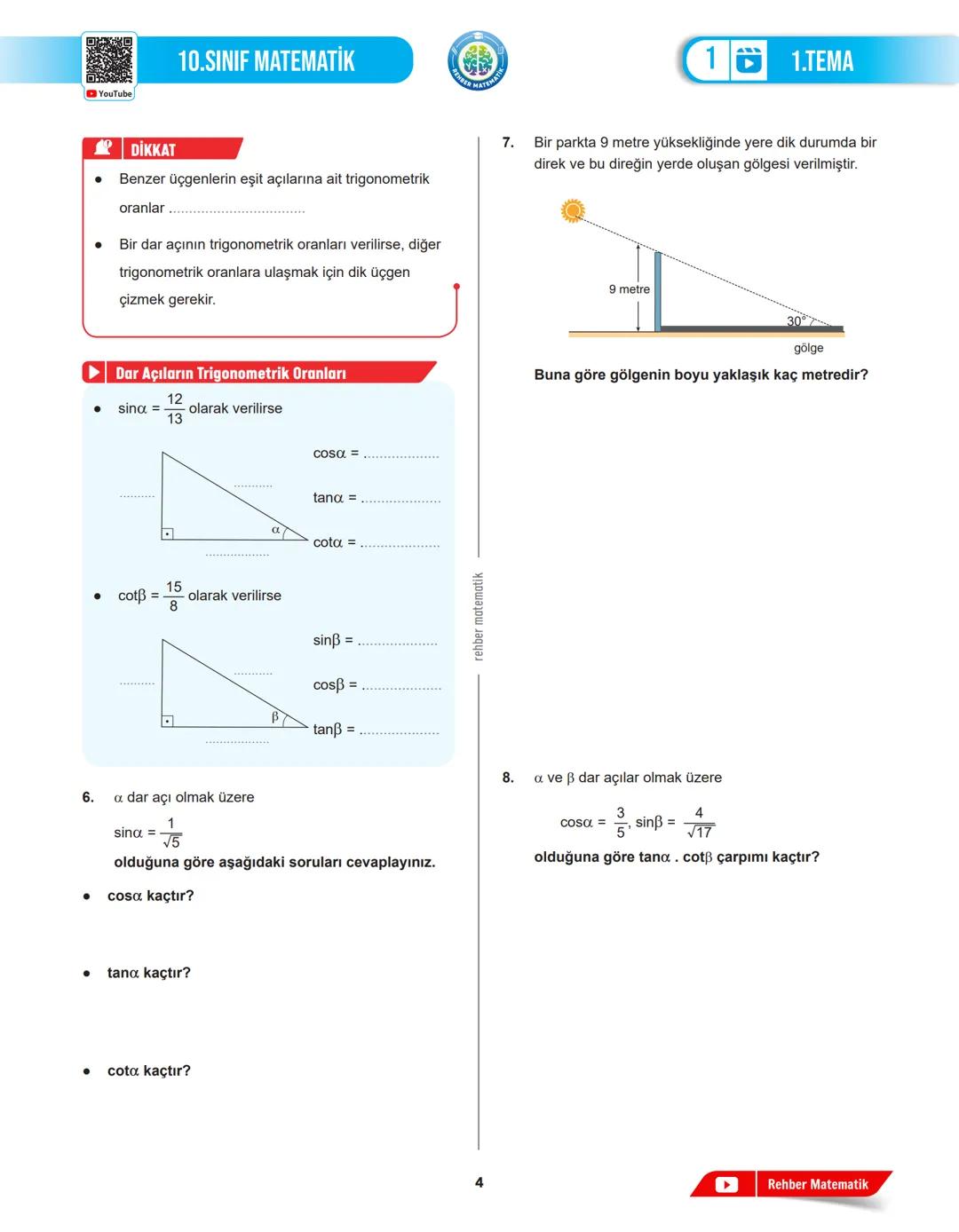
İlk olarak, problemi dikkatlice oku ve verilen bilgileri düzenle. Hangi açıların ve kenarların bilindiğini, hangilerinin istendiğini belirle. Problemin çizimini yapmak genellikle büyük yardım sağlar. Örneğin, bir üçgenin açısını bulmak için kenarları çizdiğinde problemi daha iyi anlayabilirsin.

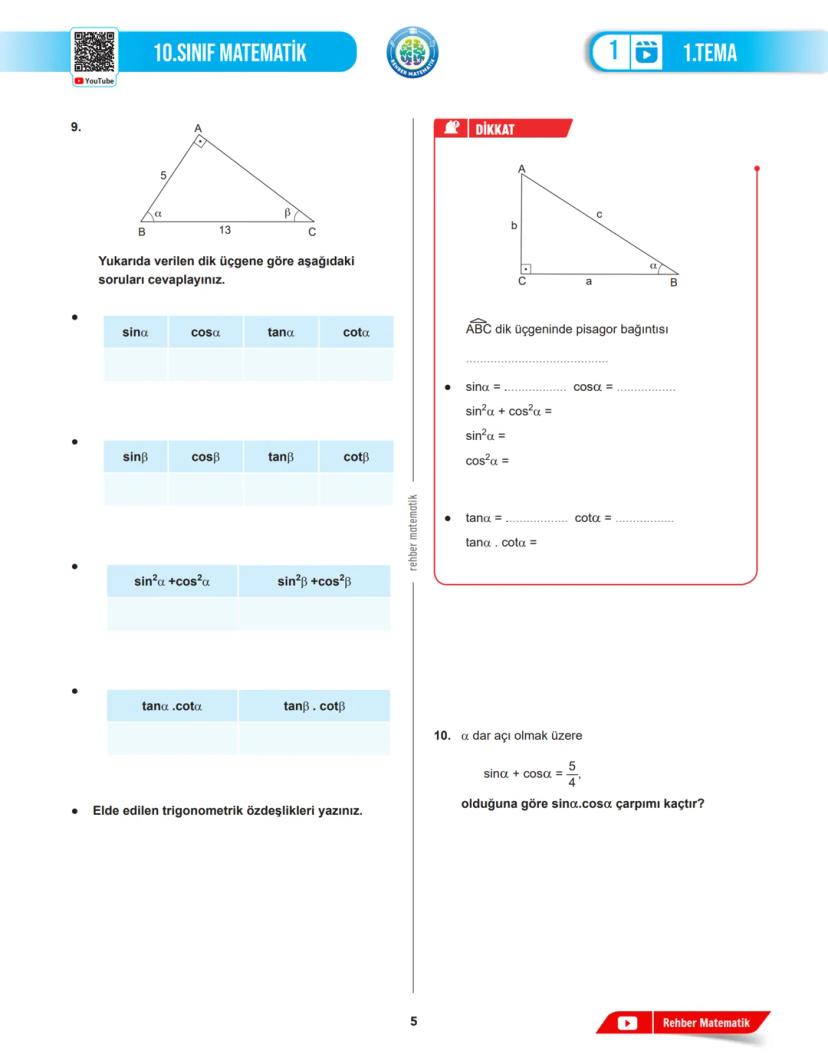
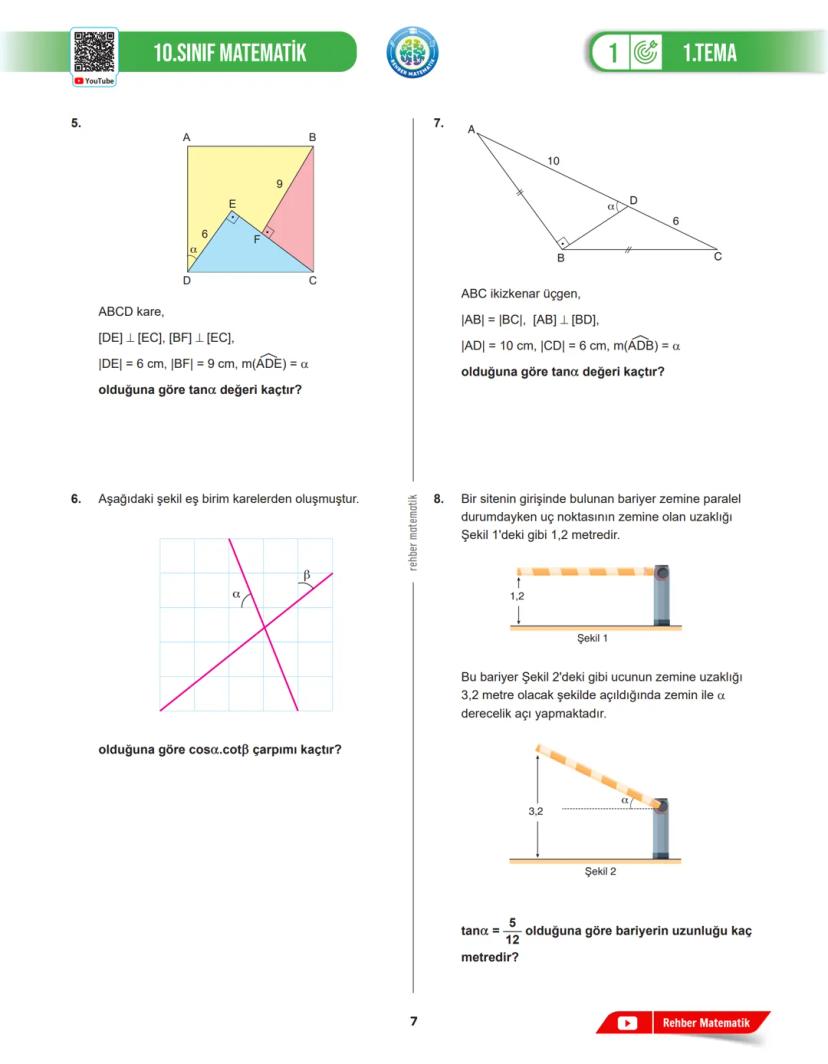
İkizkenar, dik veya benzer üçgenler gibi özel durumlara dikkat et. Bu özel durumlar, problem çözümünü büyük ölçüde kolaylaştırabilir. Örneğin, ikizkenar üçgenlerde iki kenar eşit olduğundan, bazı trigonometrik değerler daha kolay hesaplanabilir.

Bazı problemlerde Pisagor teoremi ile trigonometriyi birlikte kullanman gerekebilir. Örneğin, bir açının sinüsü verildiğinde, diğer trigonometrik oranları bulmak için a²+b²=c² formülünü kullanabilirsin.

Gerçek hayat problemlerinde, problemi matematiksel olarak modellemen gerekir. Bir bariyerin açıldığındaki durumu veya bir binanın gölgesini hesaplarken, problemi uygun bir dik üçgene dönüştürüp trigonometrik oranları kullanabilirsin.

💡 Çözüm Taktiği: Problem çözerken zorlanıyorsan, bilinmeyen değişkeni temsil eden bir üçgen çiz ve bildiğin kenarları veya açıları işaretle. Sonra uygun trigonometrik oranı seç ve denklemi kur. Bu yaklaşım, karmaşık problemleri adım adım çözmeyi kolaylaştırır.