Paralelkenar ve Özellikleri
Paralelkenar, karşılıklı kenarları birbirine paralel olan dörtgenlerdir. Kapılar, pencereler, hatta bazı mobilya tasarımları paralelkenar şeklindedir.
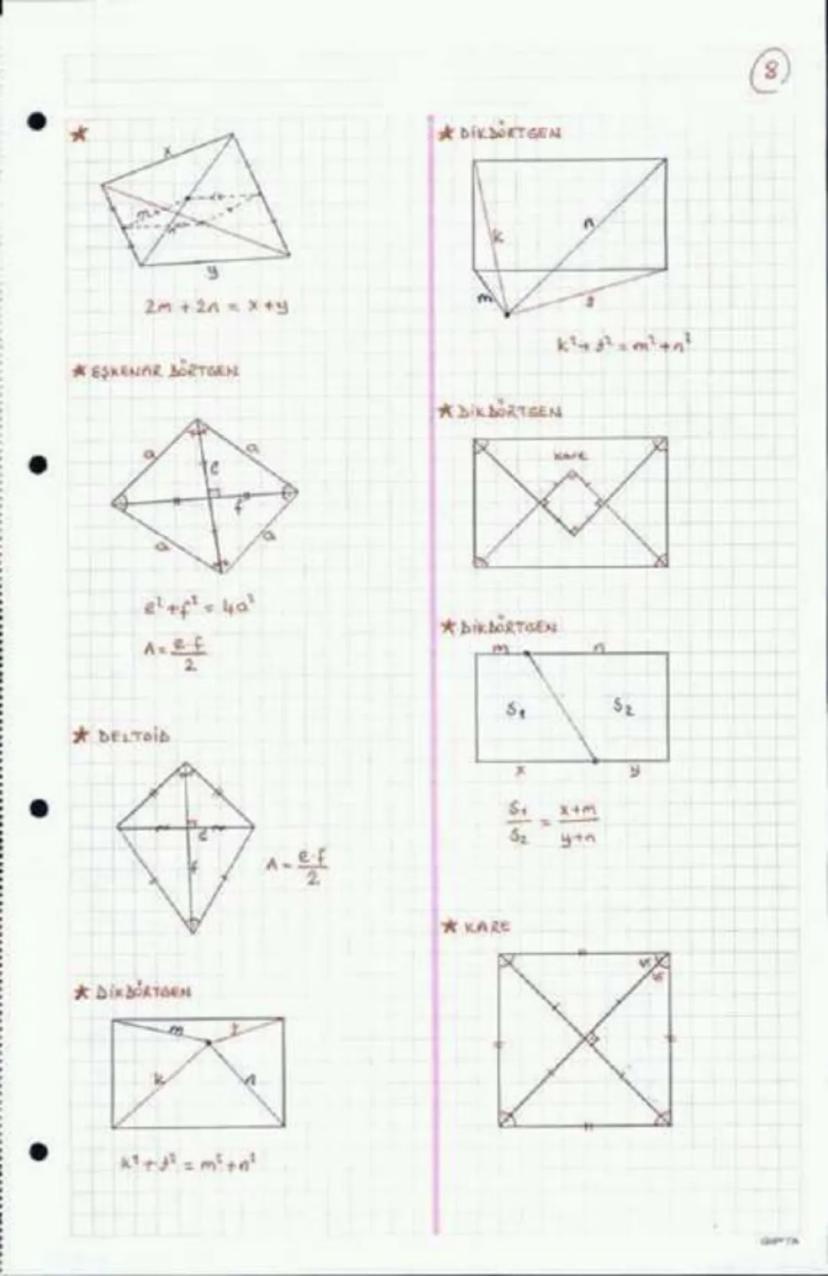
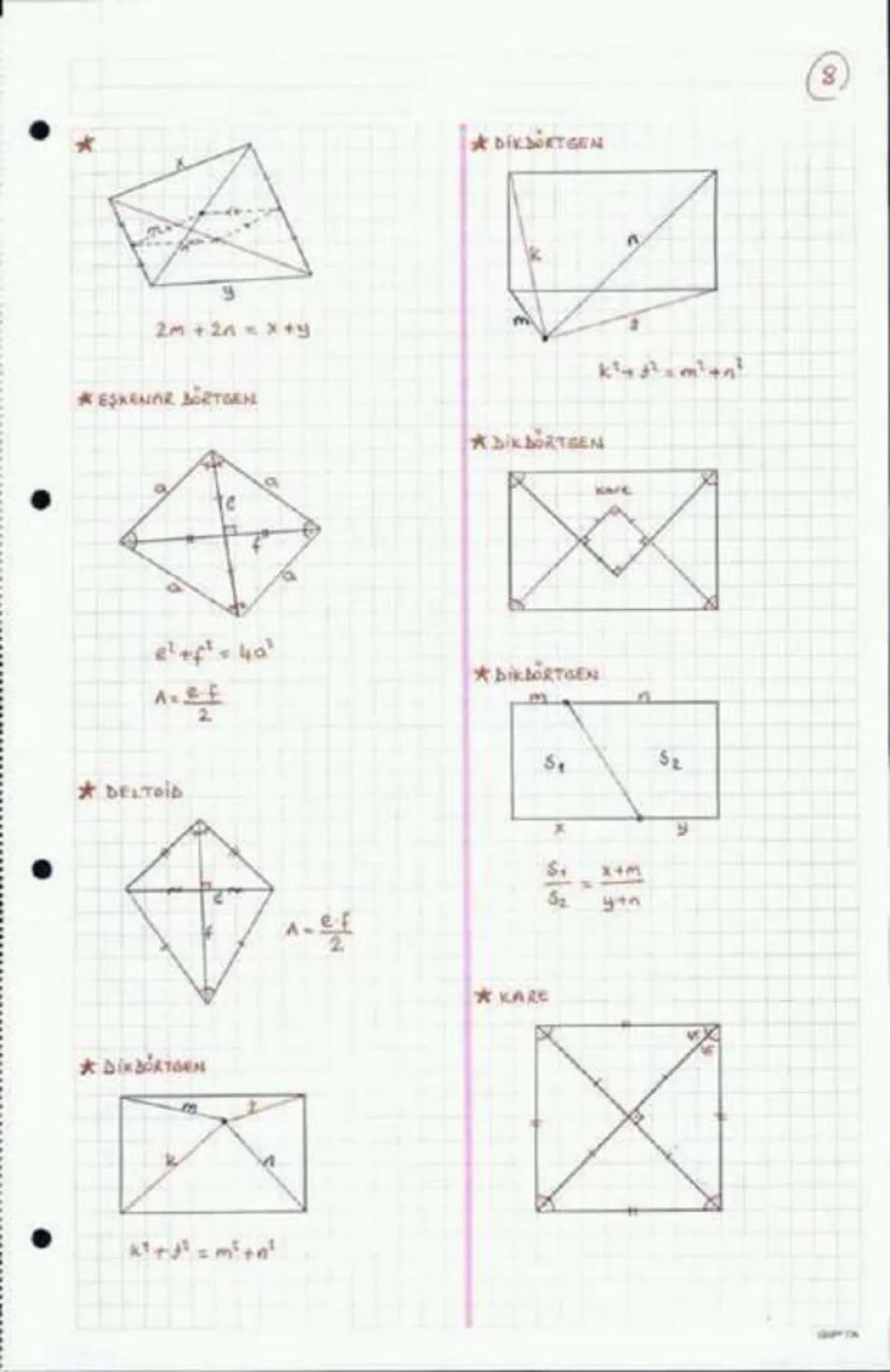
Paralelkenarın karşılıklı kenarları birbirine eşittir a=c,b=d. Köşegenleri birbirini ortalar ve bu özellik, paralelkenarı tanımlamak için kullanılabilir.
Alan hesaplarken taban×yükseklik formülü A=a×h kullanılır. Ayrıca, paralelkenarın alanı, köşegenleri e ve f ile sinüs değerini kullanarak da hesaplanabilir: Alan = (e×f×sinθ)/2 burada θ köşegenlerin arasındaki açıdır.
💡 Paralelkenar, dörtgenler ailesinin çok özel bir üyesidir. Tüm açıları 90° olursa dikdörtgene, tüm kenarları eşit olursa eşkenar dörtgene, hem açıları 90° hem de kenarları eşit olursa kareye dönüşür!