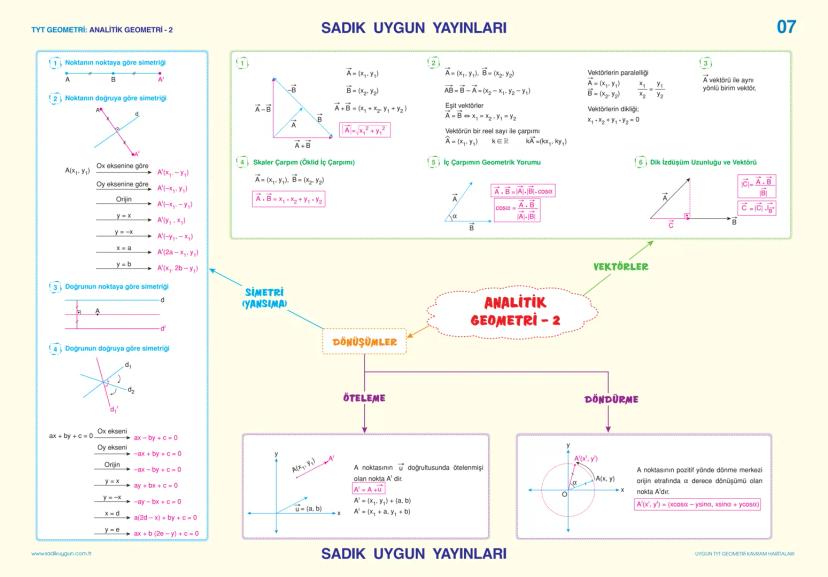
Analitik Geometri - 2
Analitik geometride simetri ve dönüşüm konuları sınavlarda karşılaşabileceğin önemli başlıklardır.
Simetri (Yansıma) kavramında bir noktanın:
- x-eksenine göre simetriği: A(x₁, y₁) → A'x1,−y1
- y-eksenine göre simetriği: A(x₁, y₁) → A'−x1,y1
- Orijine göre simetriği: A(x₁, y₁) → A'−x1,−y1
Doğruların simetriğini alırken de benzer kurallar geçerlidir. Örneğin ax + by + c = 0 doğrusunun x-eksenine göre simetriği: ax - by + c = 0 şeklinde olur.
Öteleme dönüşümünde, bir nokta belirli bir vektör doğrultusunda kaydırılır:
A(x, y) → A'x+a,y+b
Döndürme dönüşümünde ise, bir nokta orijin etrafında α açısı kadar döndürülür:
A(x, y) → A'xcosα−ysinα,xsinα+ycosα
Önemli! Sınavda simetri soruları genellikle şekil çizmeden çözülebilir. Formülleri iyi bilirsen bu tür soruları hızlıca çözebilirsin.
Vektörler konusunda, bir vektörün büyüklüğünü |A| = √x12+y12 formülü ile hesaplayabilirsin.
İki vektörün skaler (iç) çarpımı, A·B = x₁x₂ + y₁y₂ formülü ile hesaplanır ve iki vektörün dikliği için A·B = 0 olması gerekir.
Vektörlerin geometrik yorumunda, iki vektörün iç çarpımı A·B = |A|·|B|·cosα şeklinde de ifade edilir. Bu formül, iki vektör arasındaki açıyı bulmak için kullanılır.
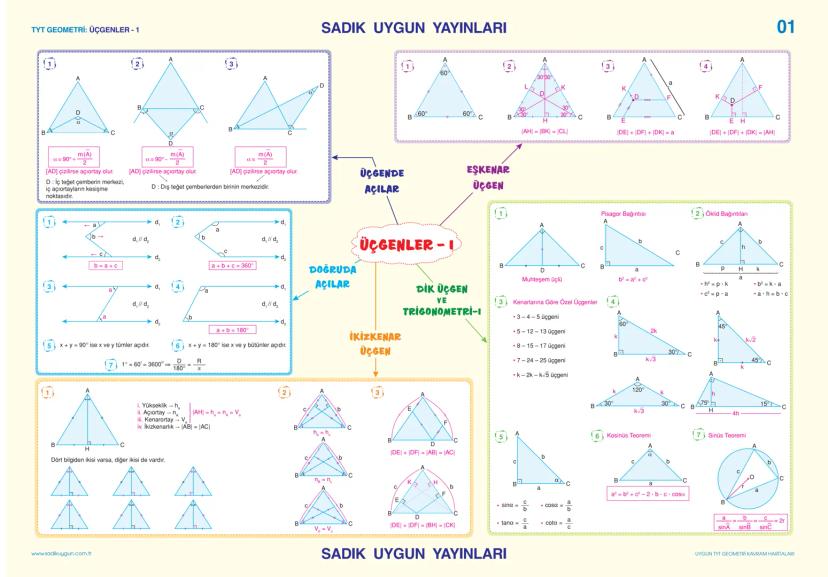
![TYT GEOMETRİ: ÜÇGENLER - 1
2
(3)
SADIK UYGUN YAYINLARI
60°
30
K
LA
D
3
F
a
KA
D
K
D
F
01
Da
BA
α=90°+\frac{m(A)}{2}
[AD] çizilirse açıortay](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0196ee73-e921-7b69-90bc-1f4048f0cf00_image_page_1.webp&w=2048&q=75)
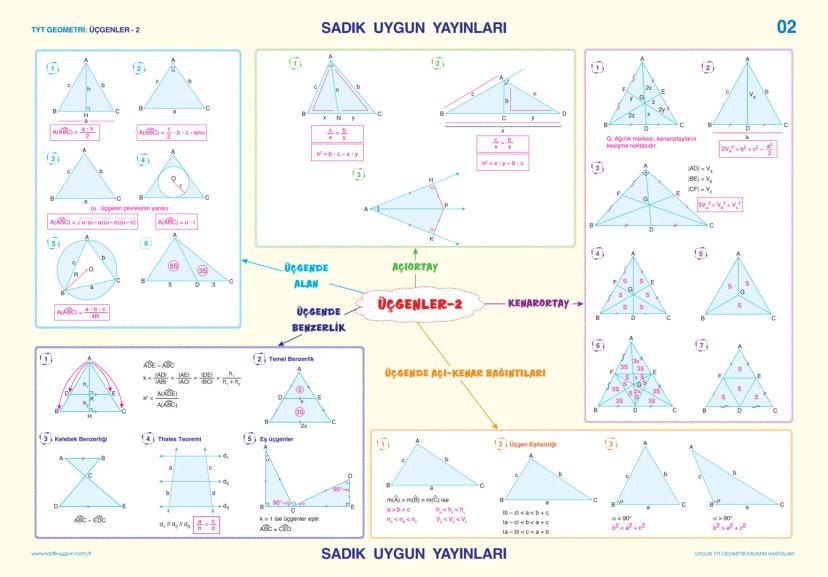
![TYT GEOMETRİ: ÜÇGENLER - 1
2
(3)
SADIK UYGUN YAYINLARI
60°
30
K
LA
D
3
F
a
KA
D
K
D
F
01
Da
BA
α=90°+\frac{m(A)}{2}
[AD] çizilirse açıortay](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0196ee73-e921-7b69-90bc-1f4048f0cf00_image_page_2.webp&w=2048&q=75)
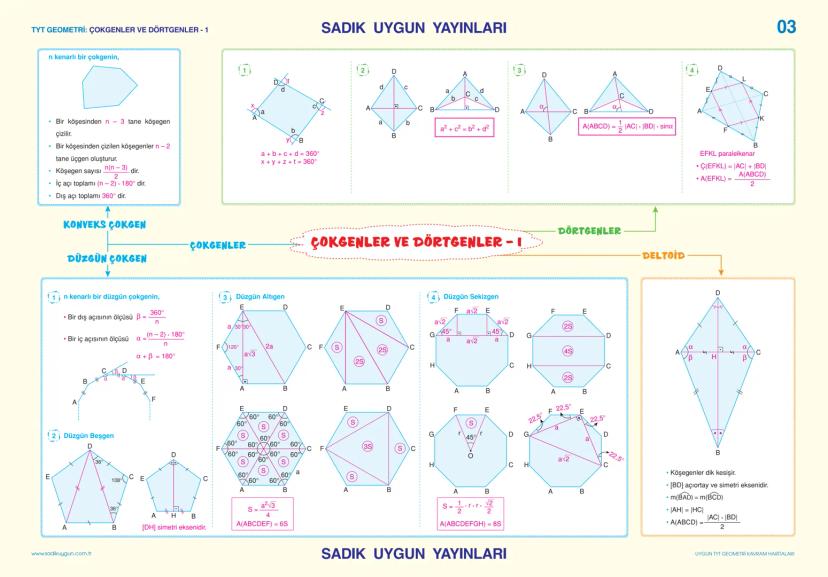
![TYT GEOMETRİ: ÜÇGENLER - 1
2
(3)
SADIK UYGUN YAYINLARI
60°
30
K
LA
D
3
F
a
KA
D
K
D
F
01
Da
BA
α=90°+\frac{m(A)}{2}
[AD] çizilirse açıortay](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0196ee73-e921-7b69-90bc-1f4048f0cf00_image_page_3.webp&w=2048&q=75)
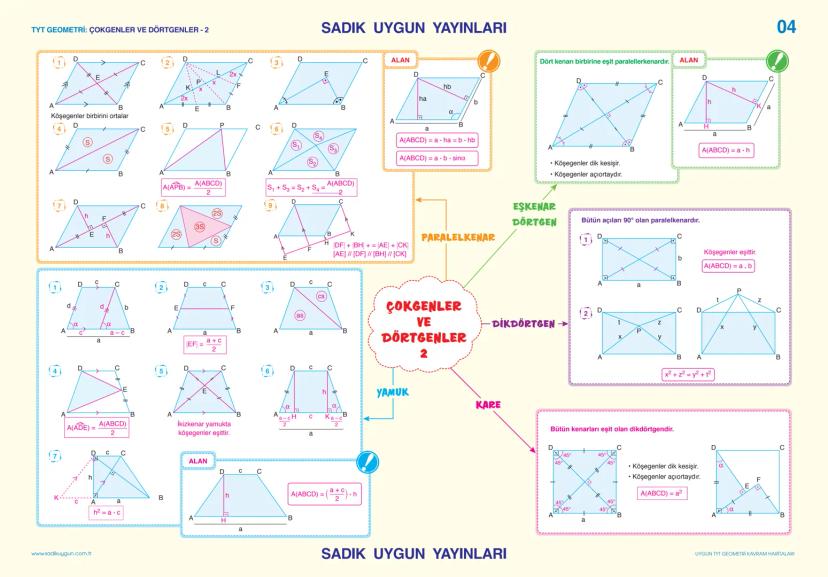
![TYT GEOMETRİ: ÜÇGENLER - 1
2
(3)
SADIK UYGUN YAYINLARI
60°
30
K
LA
D
3
F
a
KA
D
K
D
F
01
Da
BA
α=90°+\frac{m(A)}{2}
[AD] çizilirse açıortay](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0196ee73-e921-7b69-90bc-1f4048f0cf00_image_page_4.webp&w=2048&q=75)
![TYT GEOMETRİ: ÜÇGENLER - 1
2
(3)
SADIK UYGUN YAYINLARI
60°
30
K
LA
D
3
F
a
KA
D
K
D
F
01
Da
BA
α=90°+\frac{m(A)}{2}
[AD] çizilirse açıortay](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0196ee73-e921-7b69-90bc-1f4048f0cf00_image_page_5.webp&w=2048&q=75)
![TYT GEOMETRİ: ÜÇGENLER - 1
2
(3)
SADIK UYGUN YAYINLARI
60°
30
K
LA
D
3
F
a
KA
D
K
D
F
01
Da
BA
α=90°+\frac{m(A)}{2}
[AD] çizilirse açıortay](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0196ee73-e921-7b69-90bc-1f4048f0cf00_image_page_6.webp&w=2048&q=75)
![TYT GEOMETRİ: ÜÇGENLER - 1
2
(3)
SADIK UYGUN YAYINLARI
60°
30
K
LA
D
3
F
a
KA
D
K
D
F
01
Da
BA
α=90°+\frac{m(A)}{2}
[AD] çizilirse açıortay](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0196ee73-e921-7b69-90bc-1f4048f0cf00_image_page_7.webp&w=2048&q=75)
![TYT GEOMETRİ: ÜÇGENLER - 1
2
(3)
SADIK UYGUN YAYINLARI
60°
30
K
LA
D
3
F
a
KA
D
K
D
F
01
Da
BA
α=90°+\frac{m(A)}{2}
[AD] çizilirse açıortay](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0196ee73-e921-7b69-90bc-1f4048f0cf00_image_page_8.webp&w=2048&q=75)