Vektörler ve Türleri

Fizikte büyüklükler skaler ve vektörel olmak üzere ikiye ayrılır. Skaler büyüklükler sadece bir sayı ve birimle ifade edilir. Örneğin 5 dakika, 2 kg elma veya 3.000 TL gibi değerler skaler büyüklüktür. Skaler büyüklükler basitçe cebirsel olarak toplanır ve çıkarılır.

Vektörel büyüklükler ise sayısal değerin yanı sıra doğrultu ve yön de içerir. Hız, ivme, kuvvet ve moment vektörel büyüklüklere örnektir. Mesela "İzmir'den Adana'ya giden otomobilin hızı 90 km/sa'tir" ifadesi bir vektörel büyüklüktür.

Bir vektör, yönlendirilmiş bir doğru parçasıdır ve ucunda bir ok ile gösterilir. Vektörün üzerine ismi yazılır ve üzerine küçük bir ok konulur. Vektörün mutlak değeri onun uzunluğunu gösterir. Vektörün uygulandığı nokta, doğrultusu ve yönü vektörün önemli özellikleridir.

Hatırlatma: Vektörleri skaler büyüklüklerden ayıran en önemli özellik, vektörlerin yön bilgisi taşımasıdır. Bu yüzden fiziksel problemleri çözerken, vektörel büyüklüklerin yönünü dikkate almayı unutmayın!

Vektör Elemanları ve Bileşenleri

Bir vektörün dört temel elemanı vardır: Uygulama noktası (vektörün başlangıç noktası), büyüklüğü (sayısal değeri), yönü (okun gösterdiği yön) ve doğrultusu (vektörün bulunduğu doğru). Bu dört özellik bir vektörü tam olarak tanımlar.

Bir vektörün koordinat eksenleri üzerindeki izdüşümlerine vektör bileşenleri denir. Bileşenleri bulmak için vektörün büyüklüğü ve eksenlerle yaptığı açının bilinmesi gerekir. Örneğin, bir F vektörünün x ekseni bileşeni Fx = F.Cosθ formülü ile, y ekseni bileşeni ise Fy = F.Sinθ formülü ile bulunur.

Eğer bir vektörün bileşenleri biliniyorsa, vektörün büyüklüğü F = √$Fx² + Fy²$ formülü ile hesaplanabilir. Bir vektör, her zaman kendi bileşenlerinin vektörel toplamına eşittir.

Örneğin, büyüklüğü 30 cm olan ve x ekseni ile 53° açı yapan bir A vektörünün bileşenleri:

• Ax = A.cos53° = 30 × 0,6 = 18 cm
• Ay = A.sin53° = 30 × 0,8 = 24 cm olarak bulunur.

Püf Noktası: Vektör bileşenlerini hesaplarken trigonometrik fonksiyonları doğru kullanmak çok önemlidir. Açıların referans eksenine göre nasıl ölçüldüğüne dikkat edin!

Vektörlerin Özellikleri

Vektörlerle yapılan işlemler normal sayılardan farklıdır. Vektörler birbirleriyle toplanabilir ve toplama işlemi değişme özelliğine sahiptir $A+B=B+A$. Bir vektör skaler bir sayı ile çarpılabilir; bu durumda pozitif skaler sadece büyüklüğü değiştirirken, negatif skaler hem büyüklüğü hem de yönü değiştirir.

Vektörler birbirleriyle skaler çarpım ve vektörel çarpım olmak üzere iki şekilde çarpılabilir. Skaler çarpımın sonucu bir sayı iken, vektörel çarpımın sonucu iki vektörün oluşturduğu düzleme dik bir vektördür.

Vektörler birbirlerine bölünemezler, ancak bir vektör başka bir vektörün büyüklüğüne bölünebilir. Bir vektörün doğrultusu, yönü ve şiddeti değiştirilmeden istenilen yere taşınabilir. Bu özellik fiziksel problemleri çözümlerken büyük kolaylık sağlar.

İki vektörün eşit olması için yönlerinin ve büyüklüklerinin eşit olması gerekir. Uygulama noktaları farklı olabilir. Bir vektörün negatifi, o vektörle aynı büyüklüğe sahip fakat zıt yönde olan vektördür.

Önemli Not: Vektörlerin bölünememesi ama skaler çarpılabilmesi, fizik problemlerinde sıkça karşılaşacağınız bir özelliktir. Bu farkı anlamak, vektör işlemlerinde ustalaşmanızı sağlayacaktır.

Vektörlerin Eşitliği ve Toplanması

İki vektörün eşit olması için yön ve büyüklüklerinin aynı olması gerekir. Bir vektörün negatifi ise o vektörün doğrultusunun tam tersi olmasıdır. Örneğin, eğer A ve K eşit vektörler ise, B ve L vektörleri bunların negatifi olabilir.

Vektörler yönü ve büyüklüğü değiştirilmeden bir yerden başka bir yere taşınabilir. Bu özellik, vektörleri daha kolay toplayabilmemize olanak sağlar. Eğer vektörün doğrultusu veya büyüklüğü değişirse, artık farklı bir vektör olur.

Birden çok vektörün vektörel toplamı olan vektöre bileşke vektör denir ve "R" ile gösterilir. Vektörlerin toplanması için üçgen kuralı, paralelkenar kuralı ve çokgen kuralı gibi yöntemler kullanılır.

Vektörler toplanırken, vektörlerin yön ve büyüklük özelliklerine dikkat edilmelidir. Toplama sonucunda elde edilen vektör, genellikle toplanan vektörlerden farklı bir yön ve büyüklüğe sahip olur.

İpucu: Vektör toplamlarını çizerken, vektörleri uç uca ekleyerek çizimle çözmek, soru çözme sürenizi kısaltabilir. Ayrıca bu yöntem, cevabınızı görsel olarak kontrol etmenize de yardımcı olur.

Vektörlerin Toplanma Yöntemleri

1. Çokgen Metodu

Birden çok vektörü toplamak için çokgen metodunda, vektörlerden biri sabit tutulur ve diğer vektörler uç uca eklenerek bir çokgen oluşturulur. İlk vektörün başlangıç noktasından son vektörün ucuna çizilen ve yönü son vektöre doğru olan vektör, bileşke vektördür. Toplama işleminde vektörlerin sırası değiştirilse bile toplam vektör değişmez.

2. Paralel Kenar Metodu

İki vektörün toplamını bulmak için paralel kenar metodunda, vektörlerin başlangıç noktaları çakıştırılır ve paralelkenar tamamlanır. Başlangıç noktasından geçen köşegen, toplam vektörün şiddetini verir. Bu yöntemde, Kosinüs teoremi kullanılarak R² = F₁² + F₂² + 2F₁F₂cosα formülü ile bileşke vektörün büyüklüğü bulunabilir.

İki vektör arasındaki açı büyüdükçe bileşke vektör küçülür. Açı sıfır dereceyken bileşke vektör maksimum, 180 dereceyken minimum değerindedir. Bileşke vektörün büyüklüğü için her zaman A-B ≤ R ≤ A+B eşitsizliği geçerlidir.

Matematik Bağlantısı: Vektör toplama yöntemleri, üçgenlerde kenar-açı ilişkisine benzer. Üçgen eşitsizliğini hatırlayın: Herhangi bir üçgende, iki kenarın uzunluğunun toplamı her zaman üçüncü kenarın uzunluğundan büyüktür.

Vektörlerin Farkı ve Uyarılar

İki vektörün farkını bulmak için, vektörlerden birinin tersi alınıp diğeriyle toplanır. Yani A-B = A+$-B$ olarak hesaplanır. Vektörlerde çıkarma işlemi, toplama işlemine benzer şekilde yapılır.

Önemli Uyarılar:

1. Bir vektör x ekseni ile çakışık veya bu eksene paralel ise, x bileşeni kendisine eşit, y bileşeni sıfırdır. Bu durum, bileşen hesaplamalarında işimizi kolaylaştırır.

2. İki vektör arasındaki açı büyüdükçe bileşke vektörün büyüklüğü küçülür. Açı sıfır dereceyken bileşke vektör maksimum değerindedir $R_max = A+B$. Açı 180 dereceyken bileşke vektör minimum değerindedir $R_min = A-B$.

3. İki vektörün bileşkesinin büyüklüğü, vektörlerin büyüklüklerinin toplamından büyük olamaz ve farklarından küçük olamaz. Yani her zaman A-B < R < A+B eşitsizliği geçerlidir.

Bu kurallar, vektörel problemlerin çözümünde temel prensiplerdir ve fizik sorularında sıkça uygulanır.

Sınavlarda Dikkat: Vektör soruları çoğu zaman temel özelliklerin uygulanmasını gerektirir. Vektörlerin maksimum ve minimum değer kurallarını bilmek, birçok soruyu hızlıca çözmenizi sağlar.

Vektör Örnekleri ve Çözümler

Örnek 1: Büyüklükleri sıfırdan farklı E ve F vektörleri için aşağıdaki bilgilerden hangisi kesinlikle doğrudur? A) Uzunlukları eşitse kesinlikle eşit vektörlerdir. B) Zıt vektörlerse E=F" dir. C) Zıt vektörlerse yönleri aynıdır. D) Zıt vektörlerse E//F dir. E) Eşit vektörlerse yönleri zıttır.

Çözüm:

• A seçeneği yanlıştır, çünkü uzunlukları aynı olan vektörler farklı yönlerde olabilir.
• B seçeneği yanlıştır, zıt vektörlerse E=-F olmalıdır.
• C seçeneği yanlıştır, zıt vektörlerin yönleri de zıt olur.
• D seçeneği doğrudur. Zıt vektörler aynı doğrultuda olup birbirine paraleldir, sadece yönleri zıttır.
• E seçeneği yanlıştır, eşit vektörlerin yönleri aynıdır.

Örnek 2: Şekildeki vektörler aynı düzlemdedir. Bu vektörlerle ilgili verilen; I. N - L + M = -K II. K/2 - M = -2L III. N + L = 3K/2 eşitliklerden hangileri doğrudur?

Cevap: Şekillerde I ve II numaralı ifadelerin doğru olduğu görülmektedir. Doğru cevap C şıkkıdır.

Test Stratejisi: Vektör sorularında, eşitlikleri kontrol etmek için vektörleri bir koordinat sisteminde çizebilir ve bileşenlerini karşılaştırabilirsiniz. Bu, karmaşık görünen soruları bile basitleştirebilir.

Vektör İşlemlerinin Uygulamaları

Vektör işlemleri fizikte pek çok alanda karşımıza çıkar. Özellikle kuvvetlerin, hızların veya ivmelerin toplanmasında vektörel hesaplamalar kullanılır. Vektörlerin toplanması ve çıkarılması, fiziksel sistemlerin davranışını anlamak için temel oluşturur.

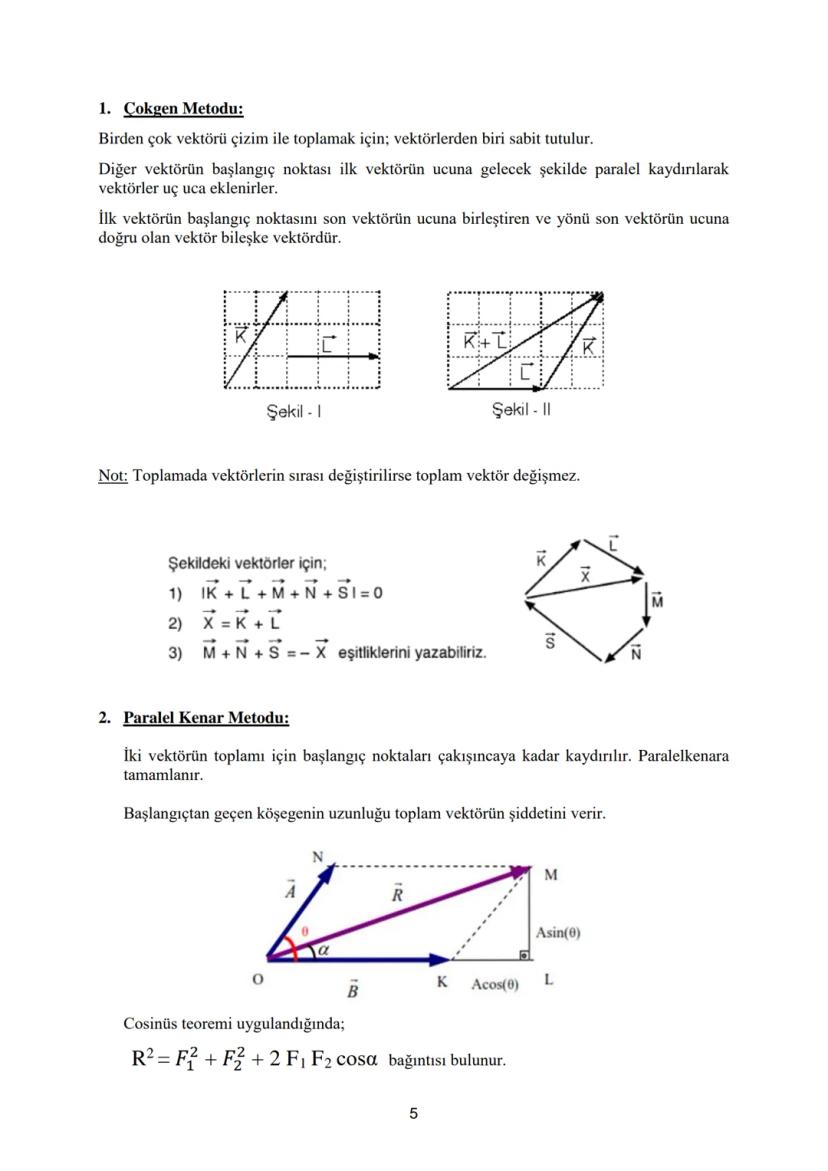
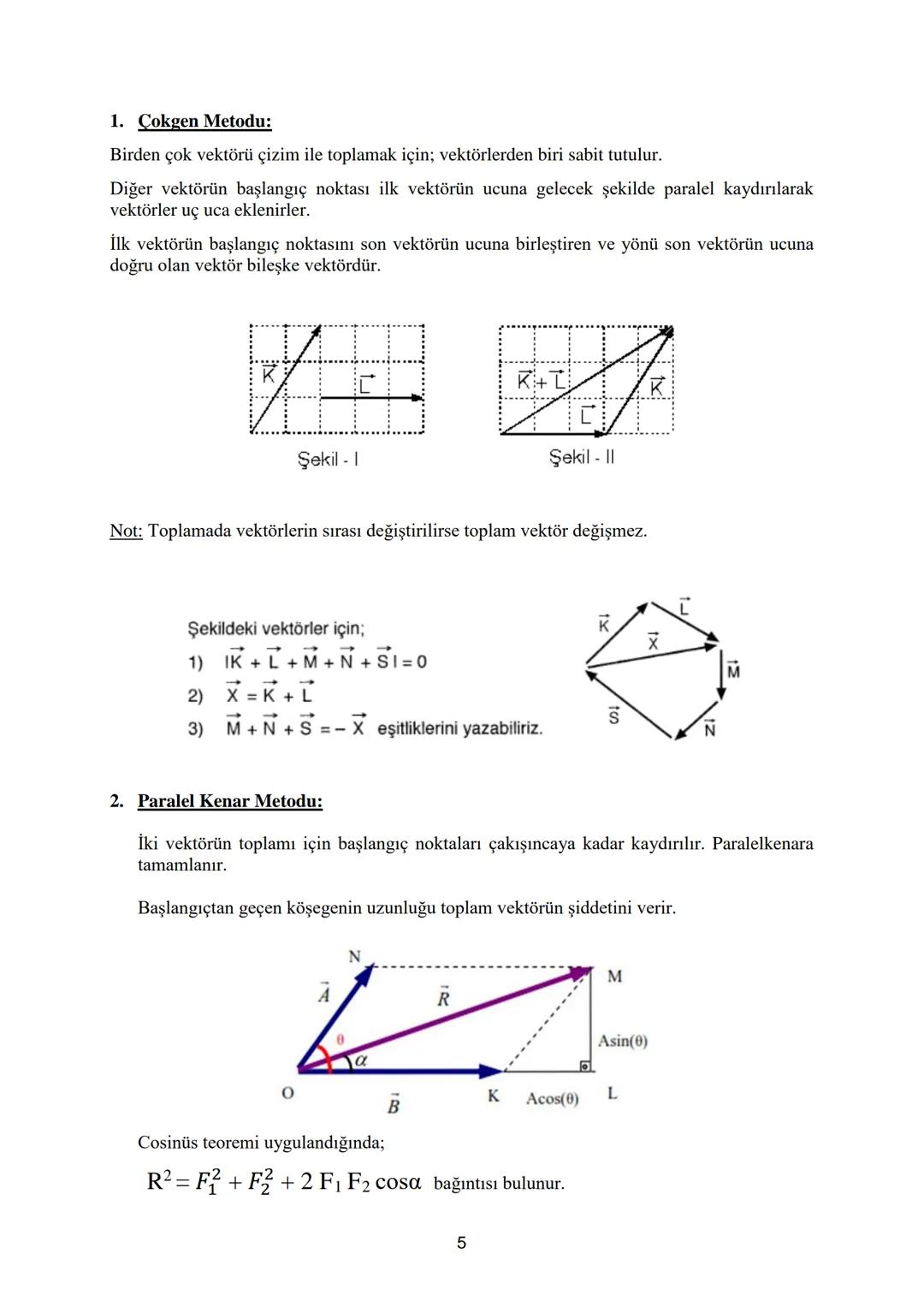
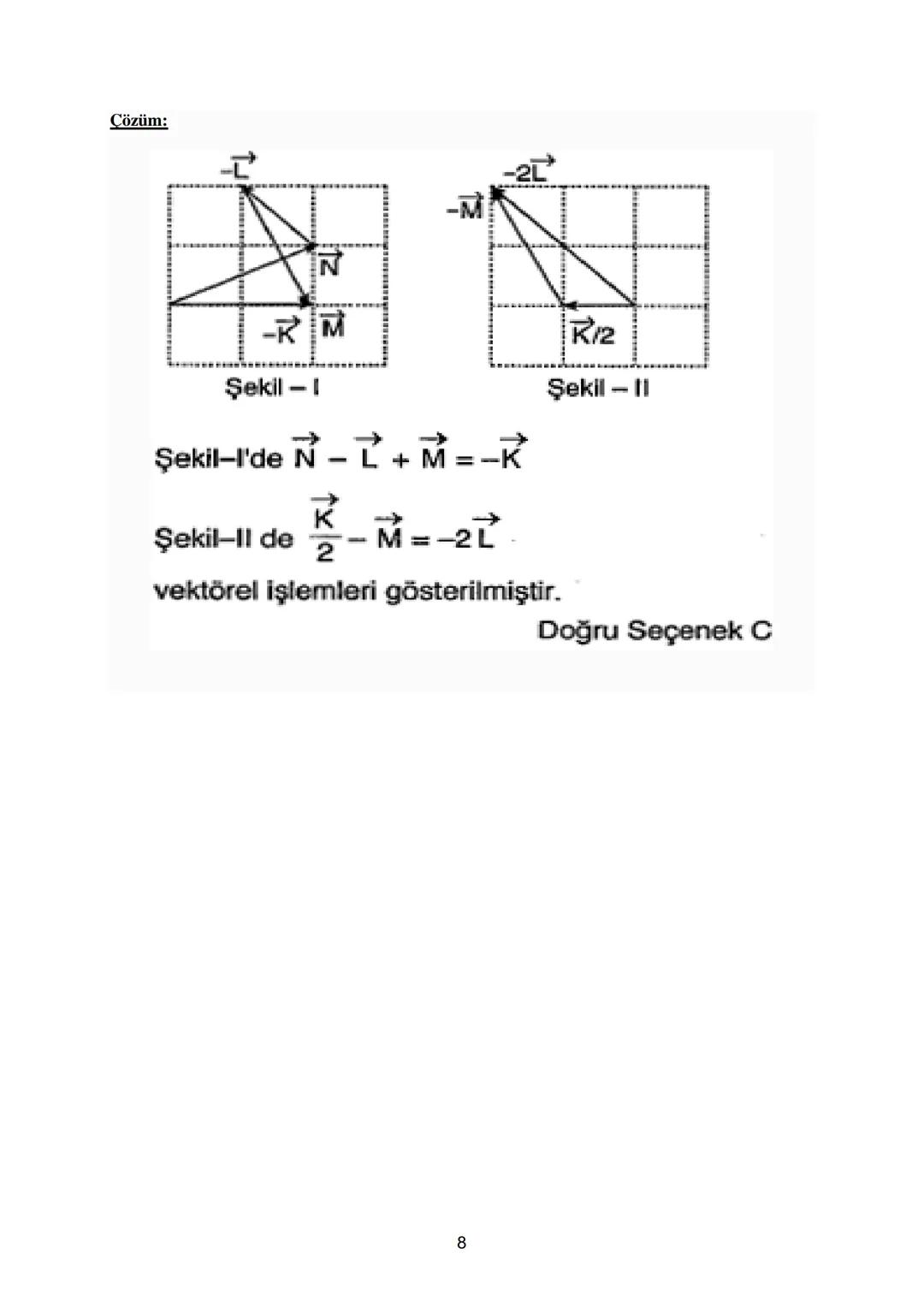
Vektör çözümlerinde çizim yapmak, problemi görselleştirmek açısından çok faydalıdır. Örnekte gösterilen şekillerde vektörel işlemlerin nasıl gösterildiğini inceleyebilirsiniz. N-L+M=-K ve K/2-M=-2L ifadelerinin doğruluğu çizimle gösterilmiştir.

Vektör problemlerini çözerken, vektörlerin bileşenlere ayrılması, toplama-çıkarma işlemlerinin yapılması ve sonucun tekrar vektör formuna dönüştürülmesi gibi adımlar izlenir. Bu süreçte trigonometrik hesaplamalar sıklıkla kullanılır.

Fizik problemlerinde vektörlerin doğru kullanılması, gerçekçi ve doğru sonuçlara ulaşmak için kritik öneme sahiptir. Bu nedenle, vektör kavramını iyi anlamak ve uygulamak, fizik derslerinde başarılı olmanın temel taşlarından biridir.

Başarı İpucu: Vektör sorularını çözerken önce ne istendiğini anlayıp, uygun metodu seçmek çok önemlidir. Bazen paralelkenar metodu, bazen çokgen metodu daha hızlı sonuca ulaşmanızı sağlayabilir.