Vektörlerin Özellikleri

Fiziksel dünyayı anlamak için iki tür büyüklük kullanırız: Sadece sayı ve birimle ifade edilen skaler büyüklükler ve bunlara ek olarak yön ve doğrultu da belirten vektörel büyüklükler. Vektörleri yönlendirilmiş doğru parçalarıyla gösteririz.

Her vektörün bir başlangıç noktası, bitiş noktası, büyüklüğü, doğrultusu ve yönü vardır. Vektörler $\vec{A}$ şeklinde gösterilir ve büyüklüğü |$\vec{A}$| veya A ile ifade edilir.

Eşit vektörler, yönü, şiddeti ve doğrultusu aynı olan vektörlerdir. Zıt vektörler ise şiddeti ve doğrultusu aynı, yönleri ters olan vektörlerdir $F₁ = -F₂$.

📌 Vektörlerin en önemli özelliği doğrultusu, yönü ve şiddeti değiştirilmeden taşınabilmeleridir. Bu sayede vektörlerle hesaplamalar çok daha kolay hale gelir!

Bir vektör bir skaler ile çarpıldığında:

• Pozitif sayıyla çarpılırsa: Büyüklüğü değişebilir, yön ve doğrultusu aynı kalır
• Negatif sayıyla çarpılırsa: Doğrultusu değişmez, büyüklüğü değişebilir ve yönü 180° döner

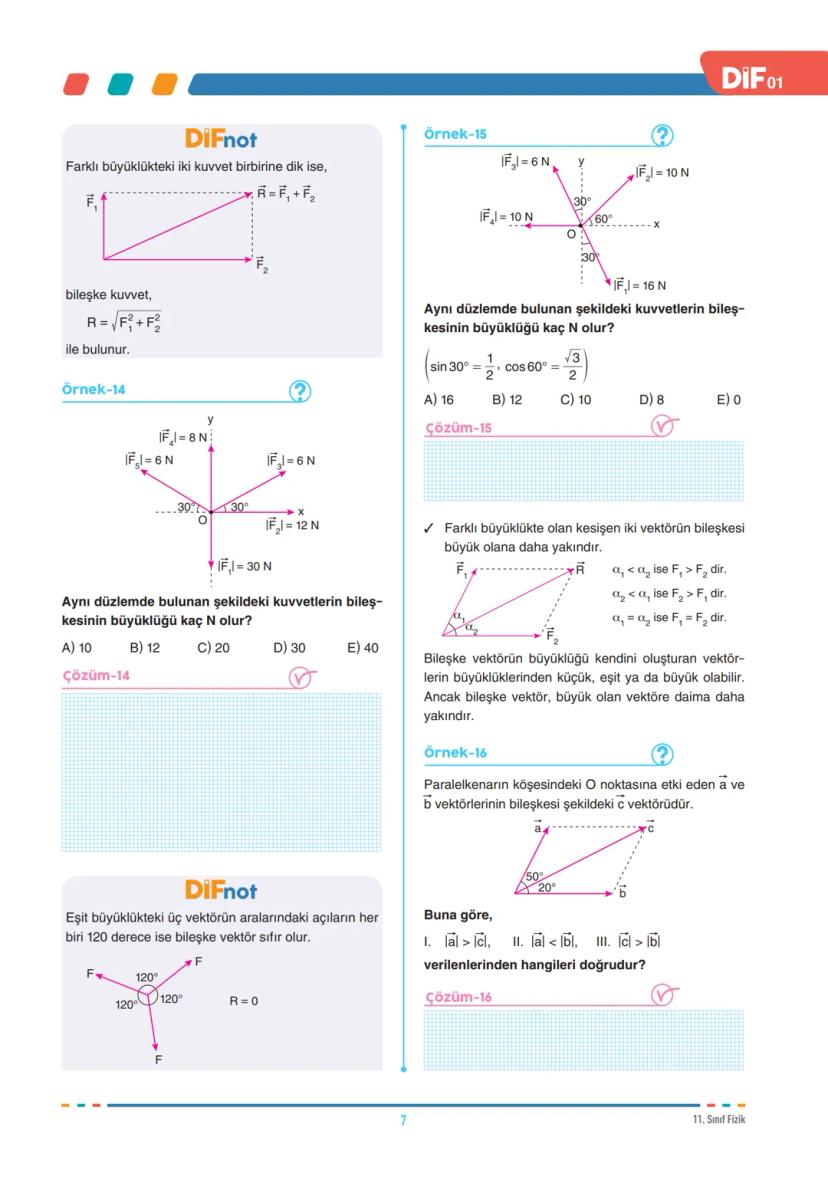
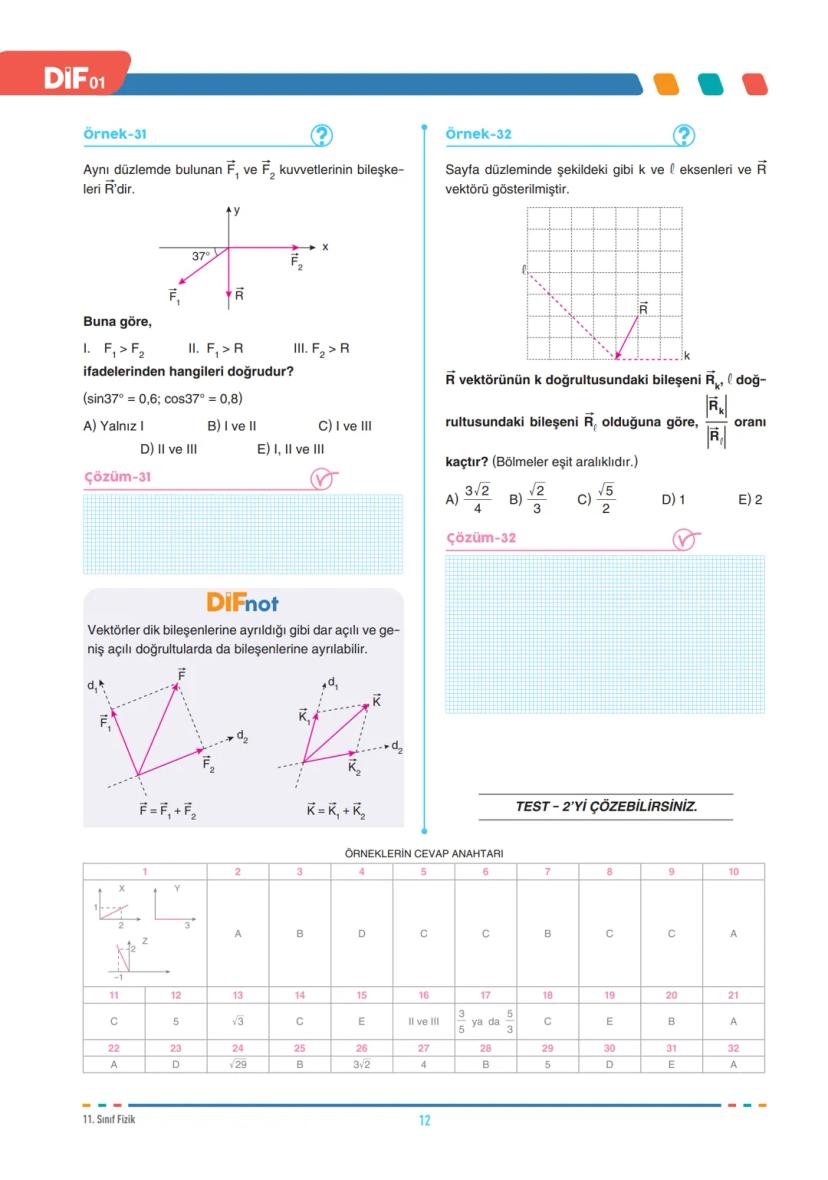
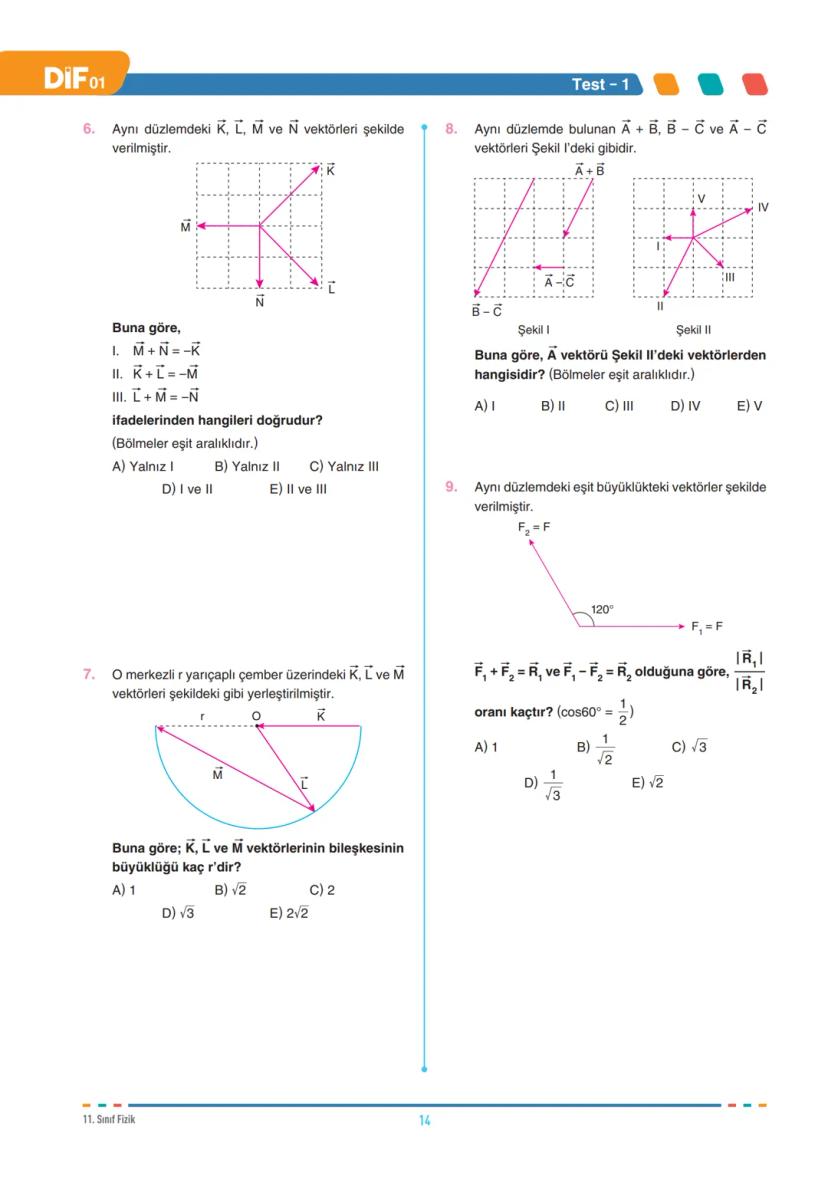
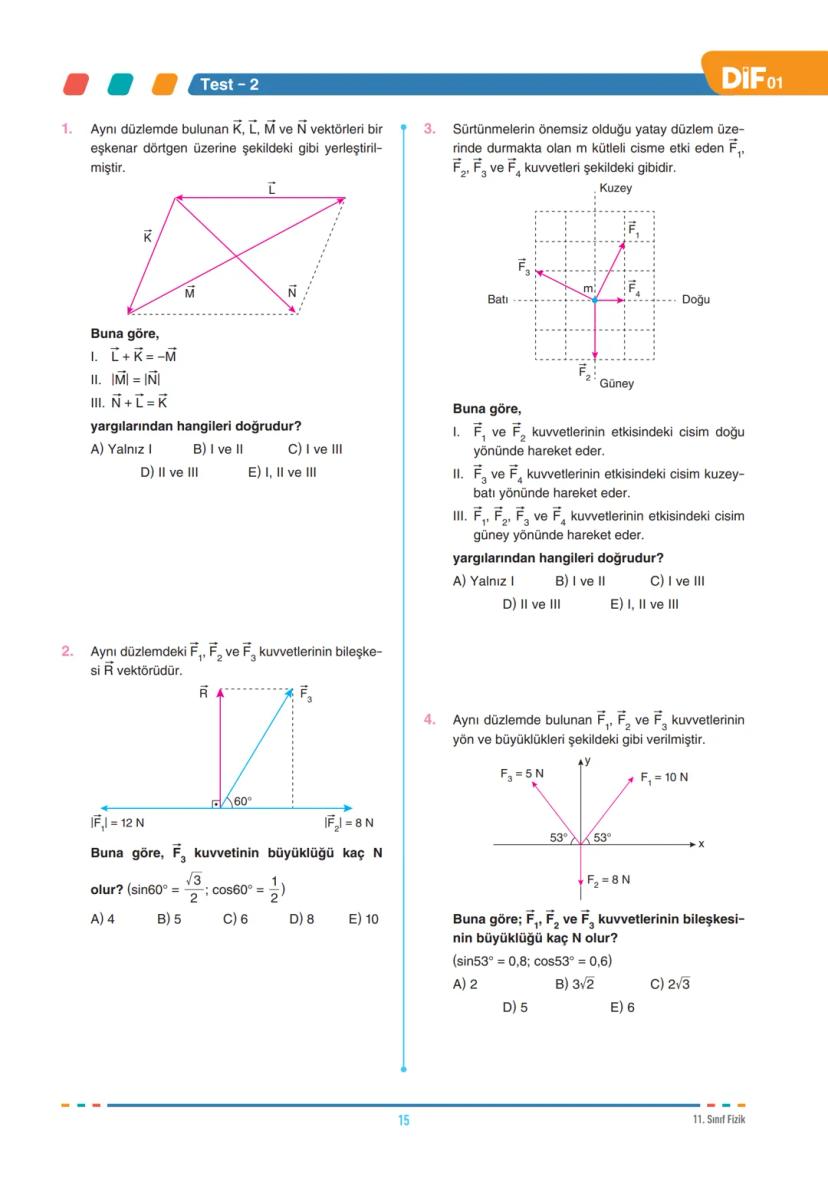
Koordinat Sisteminde Vektör Çizimi

İki boyutlu kartezyen koordinat sisteminde bir vektörü çizerken, vektörün başlangıç noktasını orijin olarak kabul ederiz. Vektörün bitiş noktası ise koordinatlarla belirtilir. Örneğin (4, 2) koordinatlarına sahip bir X vektörü, orijinden bu noktaya çizilmiş ok ile gösterilir.

Üç boyutlu sistemde de aynı mantık geçerlidir, sadece bir z koordinatı daha eklenir. Örneğin (4, 2, 1) koordinatlarına sahip bir Y vektörü, orijinden bu uzay noktasına çizilen ok ile gösterilir.

Vektörlerin Bileşkesi

Birden fazla vektörün toplanmasıyla elde edilen vektöre bileşke vektör denir ve $R$ ile gösterilir. İki temel yöntem vardır:

1. Uç Uca Ekleme Yöntemi: Bir vektörün başlangıç noktası, diğerinin bitiş noktasına gelecek şekilde yerleştirilir. Bileşke, ilk vektörün başlangıç noktasından son vektörün bitiş noktasına çizilen vektördür.

📌 Vektörlerin toplanmasında sıra önemli değildir, değişme özelliği geçerlidir. Ancak çıkarmada bu özellik yoktur!

Eğer vektörler uç uca eklendiğinde bir kapalı şekil oluşuyorsa (son vektörün ucu ilk vektörün başlangıcına ulaşıyorsa), bileşke vektör sıfırdır.

Vektör İşlemleri ve Uygulamaları

Vektörlerin Çıkarılması: Vektör çıkarma işlemi, bir vektör ile diğer vektörün tersinin toplanmasıdır: $\vec{A} - \vec{B} = \vec{A} + (-\vec{B})$

Çıkarma işleminde değişme özelliği yoktur, yani $\vec{A} - \vec{B} \neq \vec{B} - \vec{A}$ olduğunu unutmayın.

Paralelkenar Yöntemi: İki vektörün bileşkesini bulmak için başka bir yöntem de paralelkenar yöntemidir. Bu yöntemde:

1. İki vektörün başlangıç noktaları aynı yere getirilir
2. Bu noktadan çıkan iki vektörle bir paralelkenar oluşturulur
3. Bileşke vektör, başlangıç noktasından paralelkenarın karşı köşesine çizilen vektördür

Bileşke Vektörün Büyüklüğünü Hesaplama: İki vektör arasındaki açı α iken bileşke vektörün büyüklüğü şu formülle hesaplanır: $R^2 = A^2 + B^2 + 2 \cdot A \cdot B \cdot \cos\alpha$

📌 Vektör toplamında başlangıç noktasının aynı olması önemlidir. Farklı kuvvetlerin bir cisme etkisini hesaplarken paralelkenar yöntemi özellikle kullanışlıdır!

Örneğin, aynı düzlemde 6 N ve 10 N büyüklüğündeki iki kuvvet arasında 60° açı varsa, bileşke kuvvetin büyüklüğünü $R^2 = 6^2 + 10^2 + 2 \cdot 6 \cdot 10 \cdot \cos60°$ formülünden hesaplayabiliriz. $\cos60° = \frac{1}{2}$ olduğundan $R = 14$ N bulunur

Özel Durumlarda Vektörlerin Bileşkesi

Bazı özel açılarda vektörlerin bileşkesi için pratik hesaplamalar yapabiliriz:

1. İki eşit büyüklükteki vektör arasındaki açı 0° ise, bileşke vektör her birinin 2 katı büyüklüğündedir
2. Açı 60° ise, bileşke vektör her birinin √3 katı büyüklüğündedir
3. Açı 90° ise, bileşke vektör her birinin √2 katı büyüklüğündedir
4. Açı 120° ise, bileşke vektör vektörlerden biriyle aynı büyüklüktedir
5. Açı 180° ise, bileşke vektör sıfırdır (vektörler birbirini yok eder)

Farklı büyüklükteki vektörler için de çeşitli kurallar uygulanabilir. Örneğin, birbirine dik iki kuvvet için Pisagor teoremi kullanılır: $\vec{R} = \sqrt{\vec{F_1}^2 + \vec{F_2}^2}$

📌 Önemli bir nokta: Farklı büyüklükte olan iki kesişen vektörün bileşkesi, her zaman büyük olan vektöre daha yakındır!

Şu gerçeği de unutmayın: İki vektörün bileşkesinin büyüklüğü, vektörlerin büyüklüklerinin cebirsel toplamından büyük ve cebirsel farkından küçük olamaz: $|F_1 - F_2| ≤ R ≤ |F_1 + F_2|$

Eşit Büyüklükteki Vektörlerin Bileşkesi

Eşit büyüklükteki vektörlerin bileşkelerini hesaplamak için özel kurallar vardır. Açıya bağlı olarak:

• α = 0° ise → R = 2A (iki katı)
• α = 60° ise → R = A√3
• α = 90° ise → R = A√2
• α = 120° ise → R = A (aynı)
• α = 180° ise → R = 0 (sıfır)

Aralarındaki açı büyüdükçe bileşke vektörün büyüklüğü azalır. Bu yüzden aynı doğrultudaki vektörler aynı yöndeyse maksimum, zıt yöndeyse minimum bileşkeyi oluştururlar.

📌 Üç eşit büyüklükteki vektörün aralarındaki açılar 120° ise, bileşkeleri her zaman sıfır olur! Bu, kuvvetlerin dengelenmesi için önemli bir ilkedir.

Vektörlerin Bileşke Büyüklüğü İçin Sınırlar: İki vektörün bileşkesinin büyüklüğü şu sınırlar içinde olmalıdır: $|F_1 - F_2| ≤ R ≤ |F_1 + F_2|$

Minimum değer: $R_{min} = |F_1 - F_2|$ Maksimum değer: $R_{max} = |F_1 + F_2|$

Bu, herhangi iki vektörün bileşkesinin, maksimum değerin (aynı yönlü olduklarında) ve minimum değerin (zıt yönlü olduklarında) arasında olacağını gösterir. Örneğin 15 N, 20 N ve 25 N büyüklüğündeki üç kuvvetin bileşkesinin maksimum değeri 60 N, minimum değeri 0 N olabilir.

Vektörlerin Yönü ve Bileşke İlişkileri

Kesişen vektörlerde, aralarındaki açı azaldıkça bileşke vektörün büyüklüğü artar. Bu nedenle aynı doğrultudaki vektörler, aynı yönde olduklarında maksimum bileşkeyi oluştururlar.

Farklı büyüklükteki kesişen iki vektörün bileşkesi, her zaman büyük olan vektöre daha yakındır. Bileşke vektör ile her bir vektör arasındaki açılara bakılarak hangi vektörün daha büyük olduğu anlaşılabilir:

$\vec{F_1}$ $\alpha_1$ $\vec{R}$ $\alpha_2$ $\vec{F_2}$

Eğer $\alpha_1 < \alpha_2$ ise $\vec{F_1} > \vec{F_2}$ dir. Eğer $\alpha_2 < \alpha_1$ ise $\vec{F_2} > \vec{F_1}$ dir. Eğer $\alpha_1 = \alpha_2$ ise $\vec{F_1} = \vec{F_2}$ dir.

📌 Dikkat! Eşit büyüklükteki iki vektör arasındaki açı 90°'den küçükse, bileşke vektörün büyüklüğü vektörlerden daha büyük olur. Açı 90° ile 180° arasındaysa, bileşke vektör daha küçük olur.

Vektörlerin bileşkesini hesaplarken, aralarındaki açıların ve büyüklüklerin bilinmesi önemlidir. Örneğin, eşit büyüklükteki üç vektör arasında 120'şer derecelik açılar varsa, bileşke vektör her zaman sıfırdır - bu dengede olma durumunu gösterir.

Vektör Bileşkelerinin Hesaplanması

Vektörlerin bileşkesini hesaplarken farklı durumlara göre kurallar uygulanır:

Vektörlerin Açısına Göre Bileşke:

• Kesişen iki vektör arasındaki açı küçüldükçe bileşke vektör büyür
• Açı 0° olduğunda (aynı yönde olduklarında) bileşke maksimum değere ulaşır
• Açı 180° olduğunda (zıt yönde olduklarında) bileşke minimum değere düşer

Açı ve Büyüklük İlişkileri: Eşit büyüklükteki vektörlerin bileşkesi açıya göre değişir. Eşit büyüklükteki iki vektör için:

• Açı 0° ile 90° arasındaysa, bileşke vektör her bir vektörden daha büyüktür
• Açı 90° ile 180° arasındaysa, bileşke vektör her bir vektörden daha küçüktür
• Açı 90° ise, bileşke vektör √2 kat büyüklüğündedir

📌 Karşılaştığınız her türlü vektör problemi, sonunda aynı temel kurallara bağlıdır. Vektörlerin açı ve büyüklük ilişkilerini anladığınızda tüm problemleri çözebilirsiniz!

Vektörlerin bileşkeleri hesaplanırken, farklı açılarda hareket eden cisimlerin hangi yönde gideceğini belirlemek için bu kurallar kullanılır. Örneğin, noktasal bir cisme üç kuvvet uygulandığında, cismi dengede tutmak için bileşke kuvvetin sıfır olması gerekir.

Vektörlerin İki Boyutlu Koordinat Sisteminde Bileşenlerine Ayrılması

Vektörleri x ve y bileşenlerine ayırmak, karmaşık vektör problemlerini çözmenin en etkili yollarından biridir. Bu süreçte:

1. Vektörü başlangıç noktası orijin olacak şekilde koordinat sistemine yerleştiririz
2. Vektörün bitiş noktasından x ve y eksenlerine paralel doğrular çizeriz
3. Bu doğruların eksenleri kestiği noktalar, vektörün yatay ve düşey bileşenleridir

Matematiksel olarak, bir K vektörünün bileşenlerini şöyle hesaplarız (K vektörünün yatay düzlemle yaptığı açı α ise):

• $K_x = K \cdot \cos \alpha$ (x bileşeni)
• $K_y = K \cdot \sin \alpha$ (y bileşeni)

Tersine, bileşenleri bilinen bir vektörün büyüklüğünü de hesaplayabiliriz: $K^2 = K_x^2 + K_y^2$

📌 Vektörleri bileşenlerine ayırmak, karmaşık problemleri basit parçalara bölmenin harika bir yoludur. Böylece her eksendeki etkiyi ayrı ayrı hesaplayıp sonra birleştirebilirsiniz!

Birden fazla vektörün bileşkesini hesaplarken, önce her vektörü bileşenlerine ayırıp, sonra aynı eksen üzerindeki bileşenleri toplayarak işlemi kolaylaştırabiliriz. Bu yöntem özellikle farklı açılarda uygulanan kuvvetlerin net etkisini bulmak için kullanışlıdır.

Vektör Bileşenlerinin Pratik Uygulamaları

Vektörleri bileşenlerine ayırma, birçok fizik probleminin çözümünde çok pratik bir yöntemdir. Özellikle farklı açılarda etki eden kuvvetlerin net etkisini hesaplamada kullanılır.

Örneğin, aynı düzlemde farklı açılardaki üç kuvvet vektörü (F₁, F₂, F₃) için her bir kuvveti x ve y bileşenlerine ayırarak toplam etkiyi hesaplayabiliriz:

1. Her vektörün x ve y bileşenlerini hesaplarız: F₁ˣ, F₁ʸ, F₂ˣ, F₂ʸ, F₃ˣ, F₃ʸ
2. X eksenindeki toplam kuvveti buluruz: F_x = F₁ˣ + F₂ˣ + F₃ˣ
3. Y eksenindeki toplam kuvveti buluruz: F_y = F₁ʸ + F₂ʸ + F₃ʸ
4. Bileşke kuvvetin büyüklüğünü hesaplarız: R = √$F_x² + F_y²$

📌 Açılı kuvvet problemlerinde trigonometrik fonksiyonları doğru kullanmak çok önemlidir. Sin ve cos değerlerini doğru açılarla eşleştirdiğinizden emin olun!

Vektörlerin kıyaslanmasında, büyüklüklerinin yanı sıra aralarındaki açı da önemlidir. Aynı büyüklükteki vektörlerin bileşkesi, aralarındaki açı küçüldükçe büyür. Eğer açı 90°'den küçükse bileşke vektör her bir vektörden büyük, açı 90°'den büyükse bileşke vektör her bir vektörden küçük olur.

Vektör Problemlerinin Çözüm Teknikleri

Karmaşık vektör problemlerini çözmek için birkaç temel yaklaşım vardır:

Bileşenlere Ayırma Yöntemi:

1. Her vektörü x ve y bileşenlerine ayır
2. Aynı eksendeki bileşenleri topla (x'leri x'lerle, y'leri y'lerle)
3. Bileşke vektörün büyüklüğünü Pisagor teoremiyle hesapla: R = √$R_x² + R_y²$

Trigonometrik Hesaplama: Açılı vektörler için, sin ve cos fonksiyonlarını kullanarak:

• x bileşeni = |F| · cos(açı)
• y bileşeni = |F| · sin(açı)

Bu yöntemleri kullanarak, örneğin 53° açıyla duran 10 N'luk bir kuvvetin yatay bileşenini şöyle hesaplayabiliriz: F_x = 10 N · cos(53°) = 10 N · 0,6 = 6 N

📌 Vektör problemlerinde başarılı olmanın sırrı, her zaman bileşenlere ayırma tekniğini akılda tutmaktır. Bu teknik, herhangi bir açıdaki herhangi bir vektörü çözmenize olanak tanır.

Vektör hesaplamalarını pratik yaparak ustalık kazanabilirsiniz. Özellikle koordinat sisteminde bileşenlere ayırma yöntemi, üniversite fizik ve mühendislik derslerinde de sıkça karşınıza çıkacak temel bir beceridir.