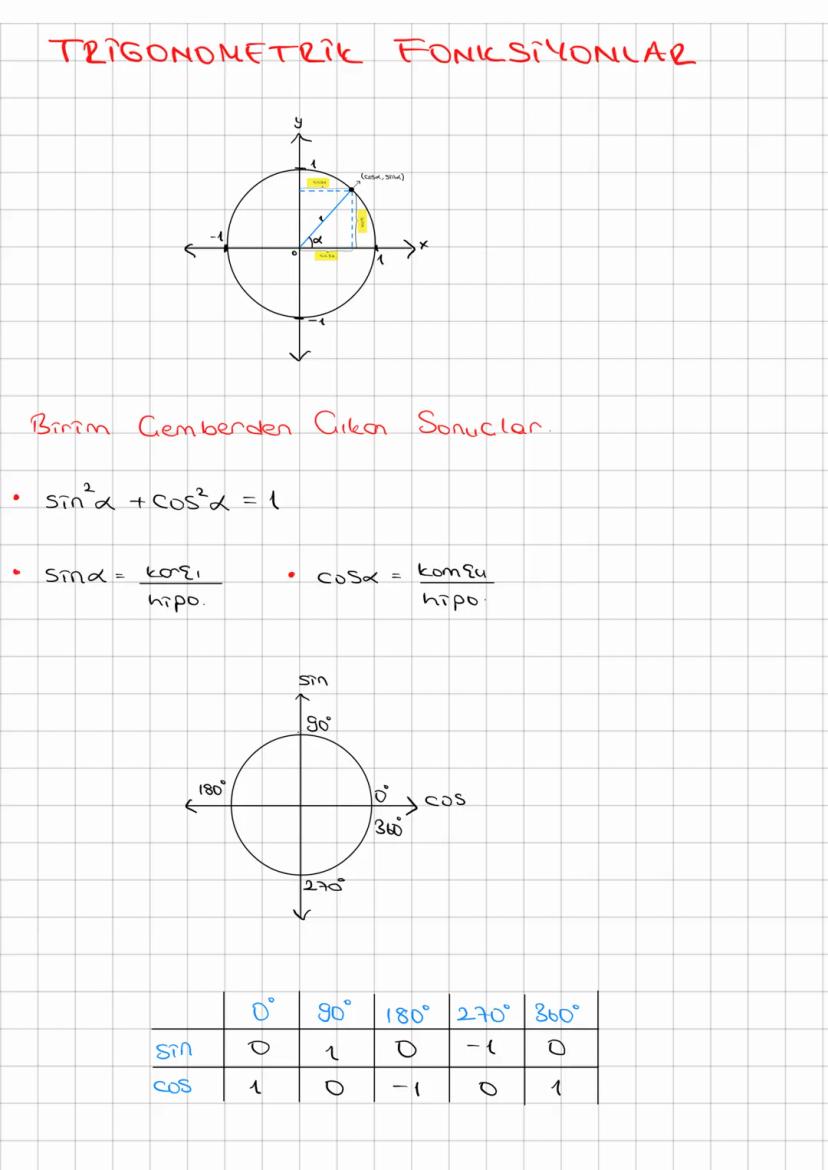
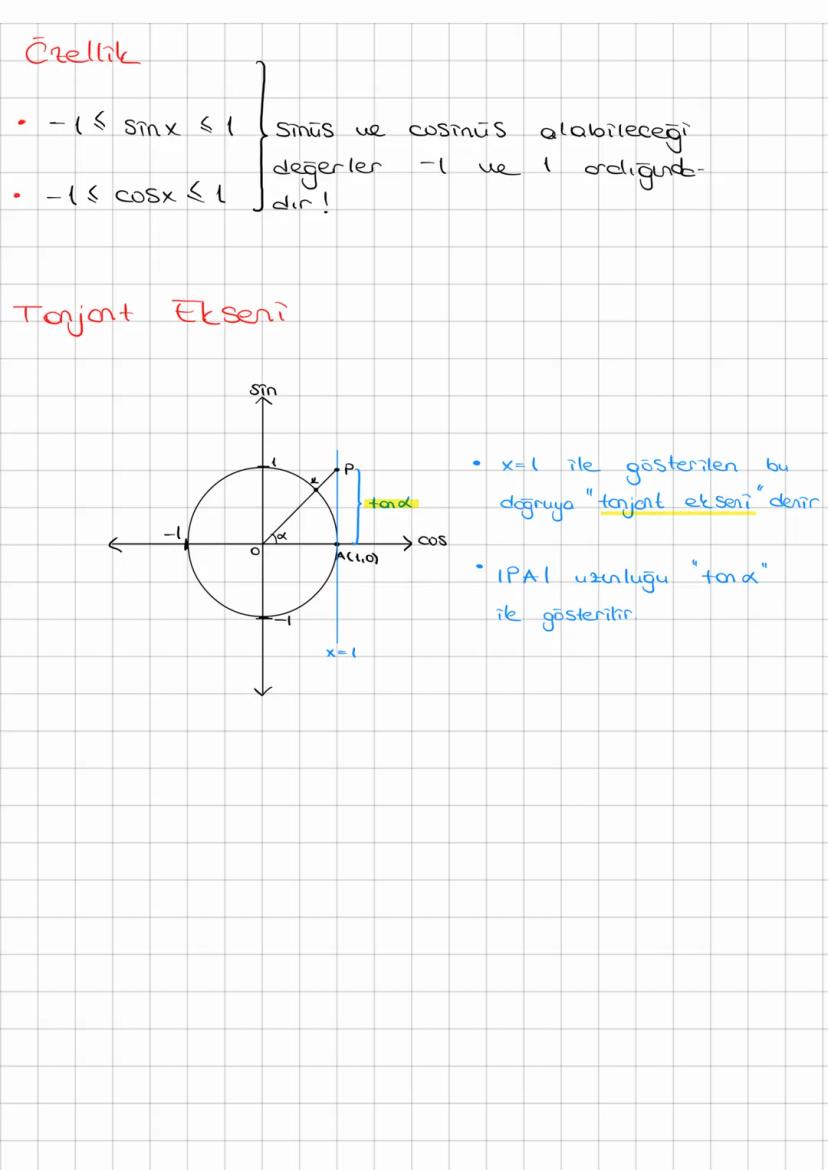
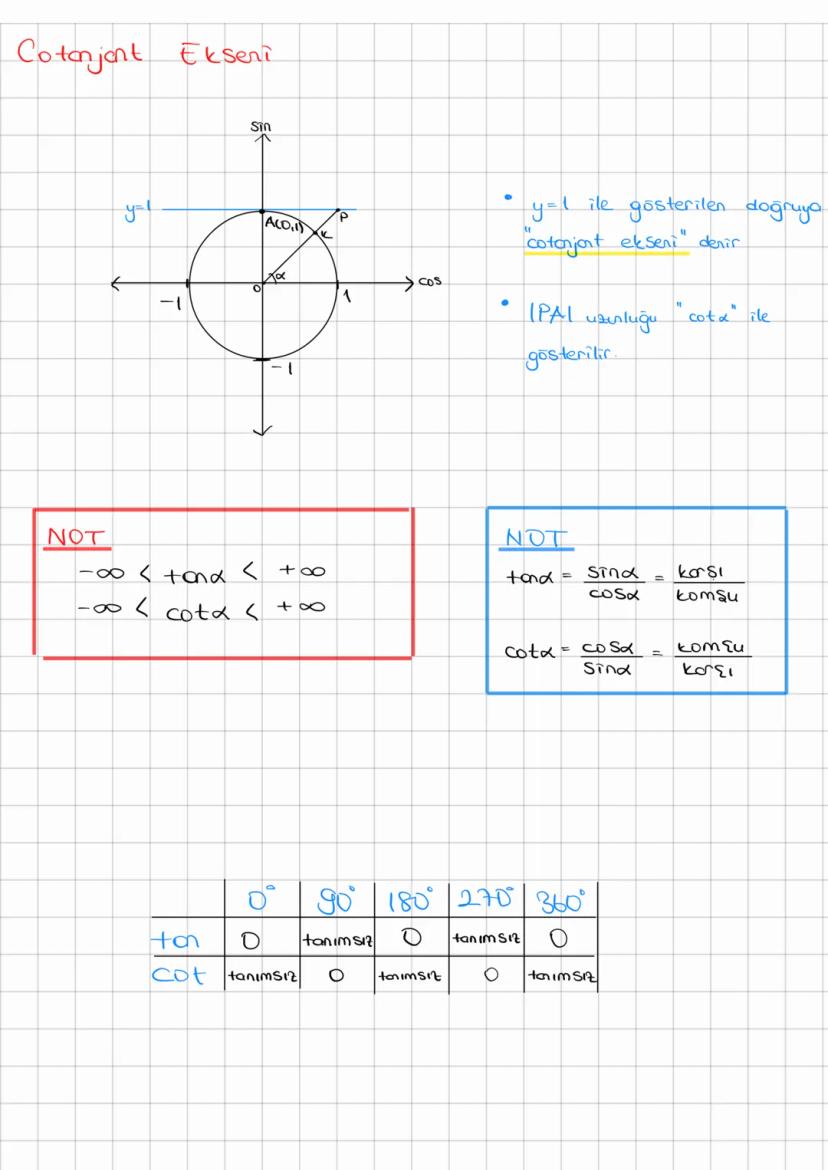
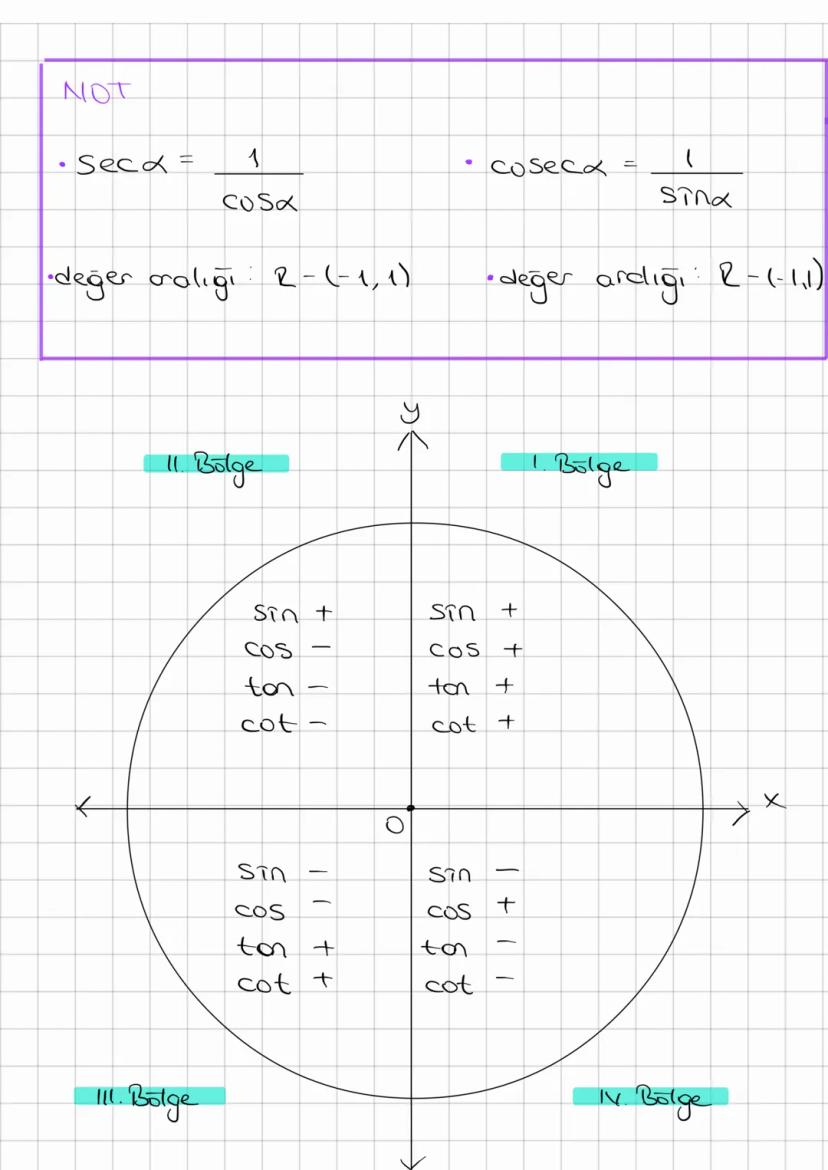
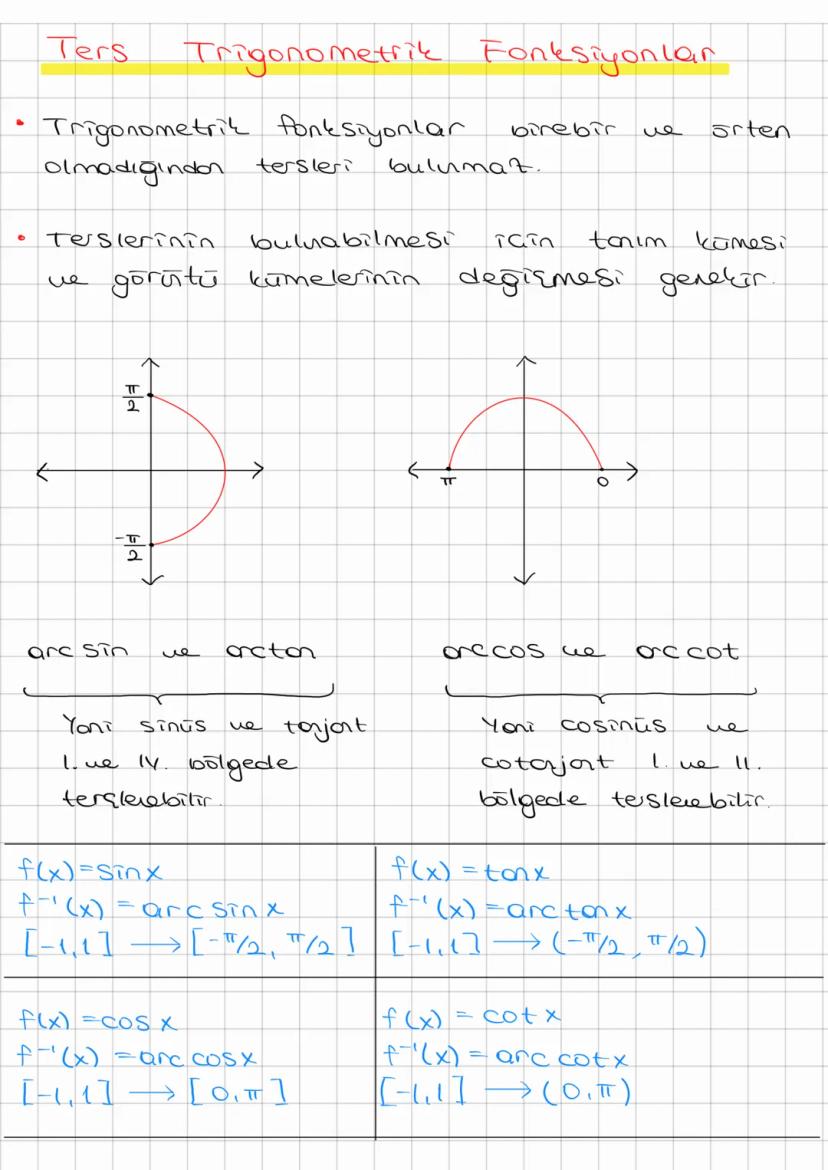
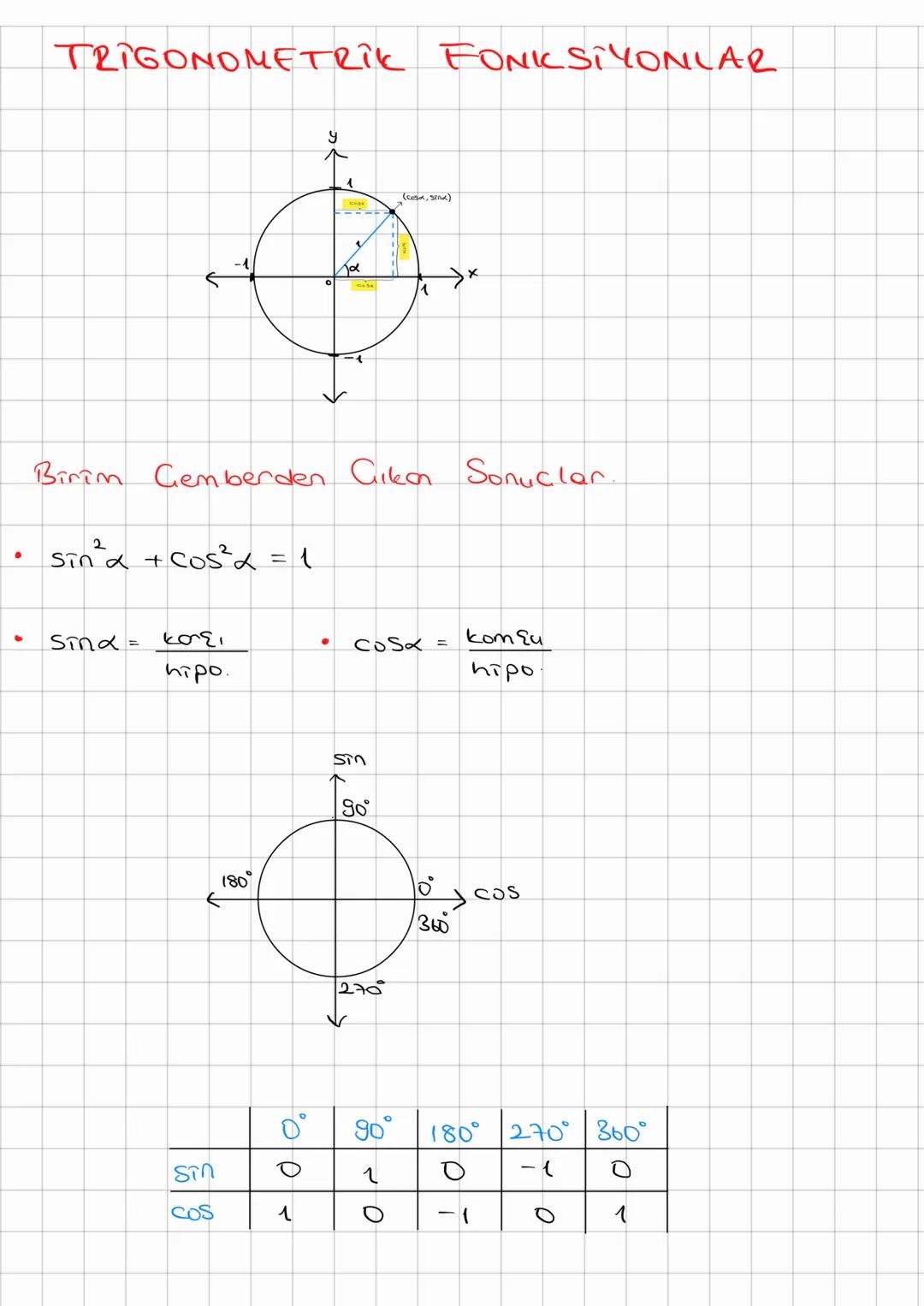
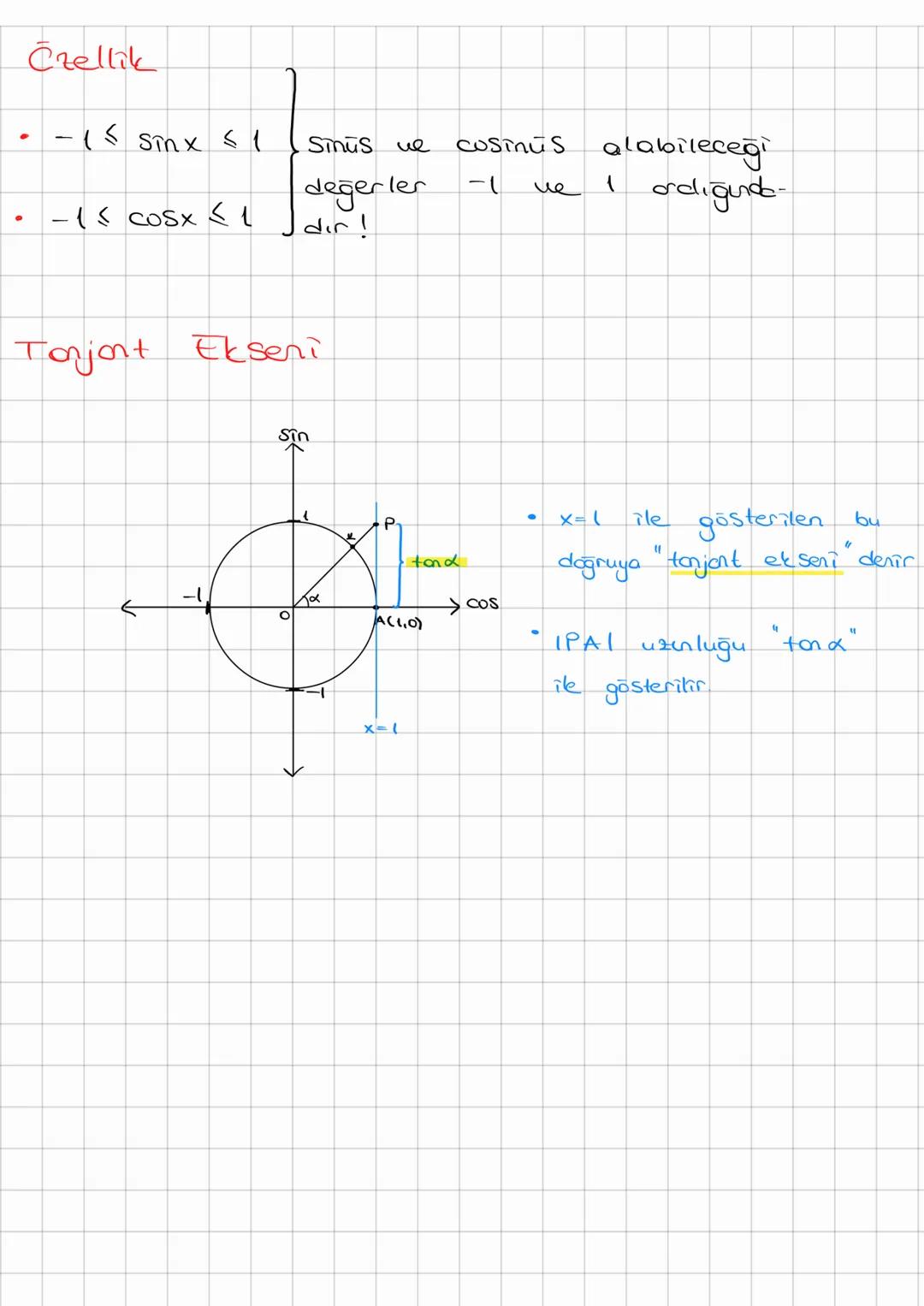
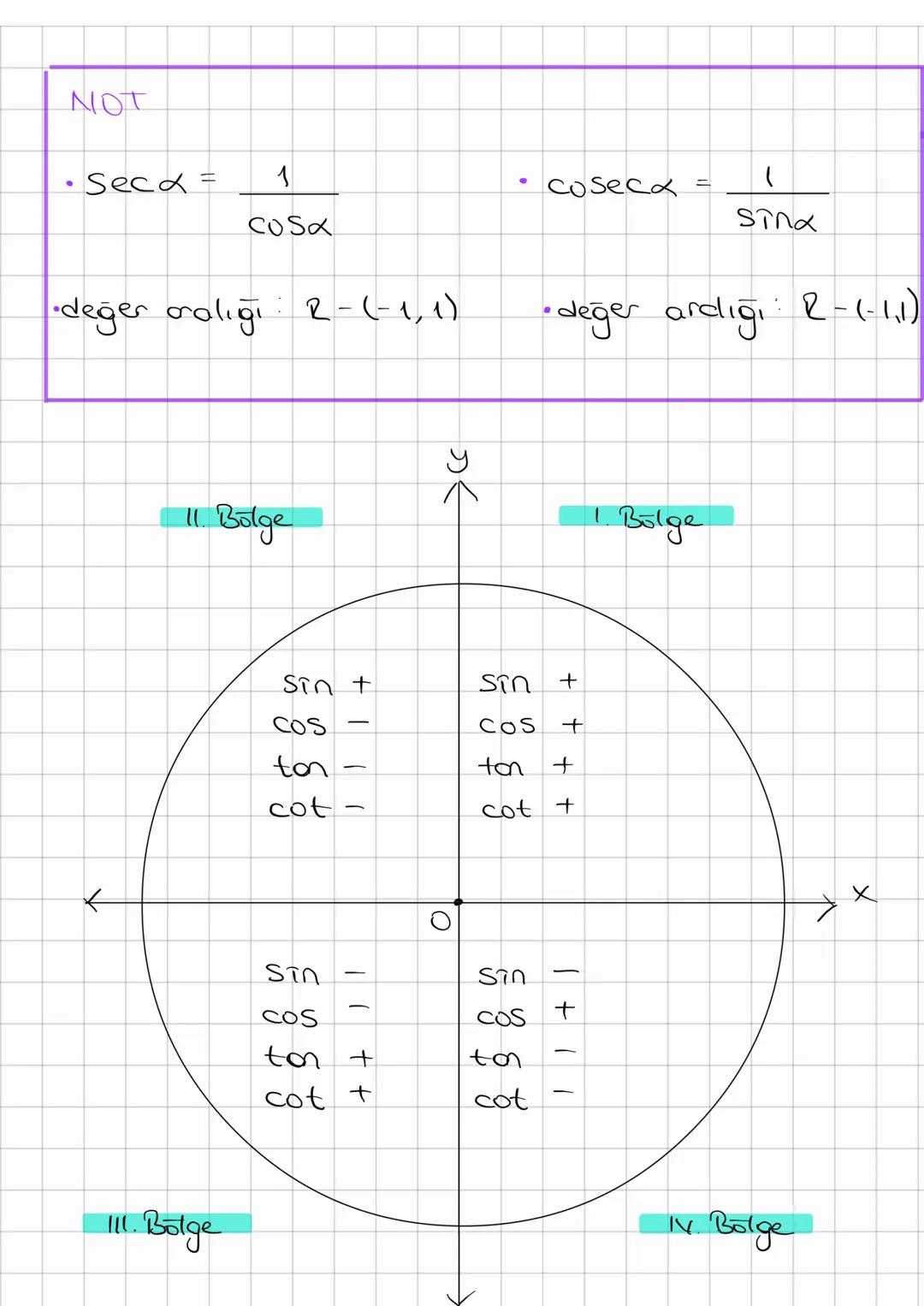
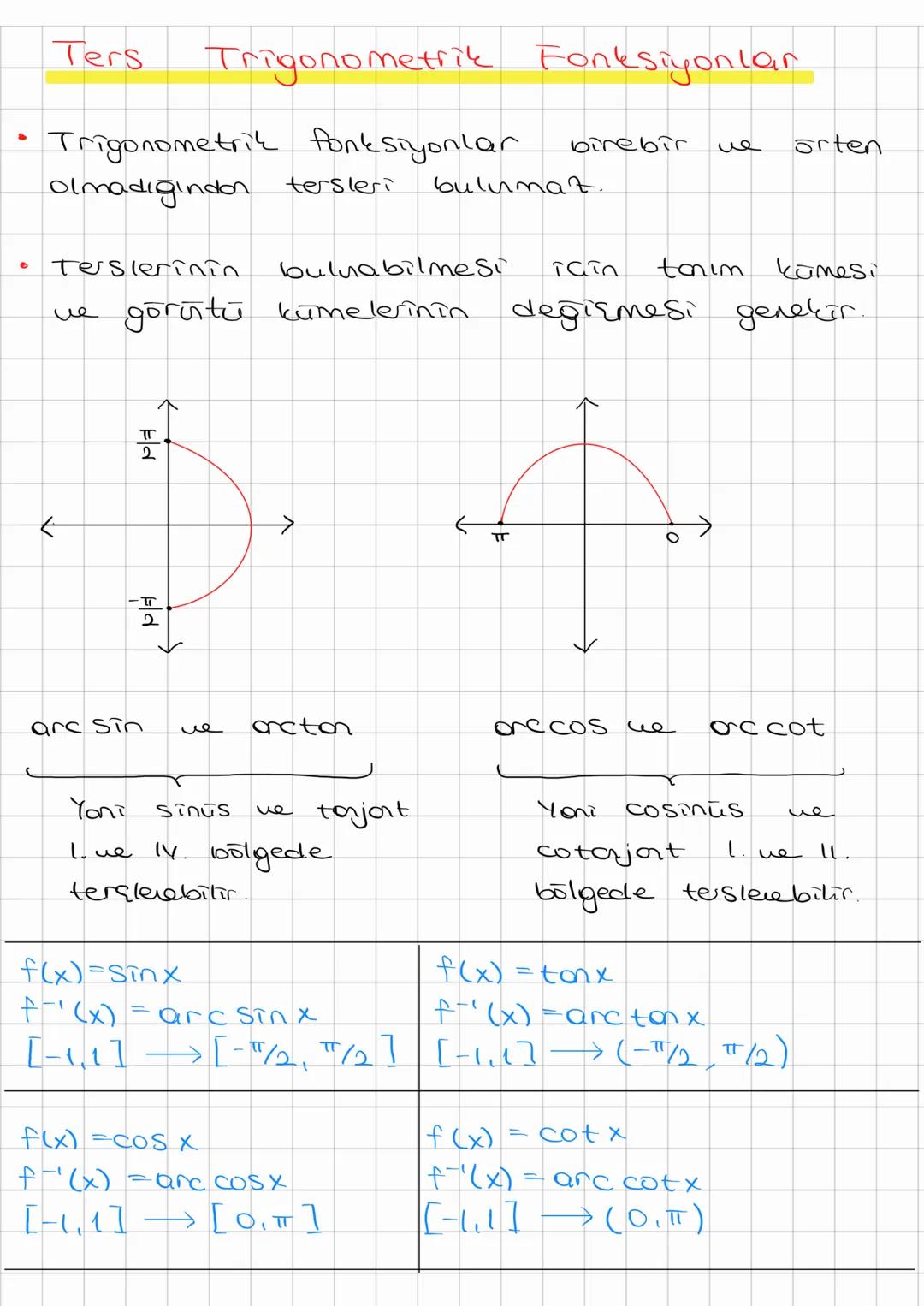
Trigonometri, açılar ve kenarlar arasındaki matematiksel ilişkileri inceleyen önemli bir... Daha fazla göster
Ders notlarını görmek için kaydolÜcretsiz!
Tüm belgeleri görebilirsin
Notlarını Yükselt
Milyonlarca öğrenciye katıl
Kaydolduğunda Hizmet Şartları ve Gizlilik Politikasını kabul etmiş olursun