Üçgenler ve Temel Özellikleri

Üçgenler, geometrinin en temel şekillerindendir. Bir üçgende iç açılar toplamı her zaman 180° ve dış açılar toplamı 360°dir. Eşkenar üçgenlerde tüm açılar 60°dir ve tüm kenarlar eşittir.

İkizkenar üçgenlerde önemli bir özellik, iki kenarın eşit olmasıdır. İkizkenar üçgenlerde yükseklik, açıortay ve kenarortay aynı doğru üzerindedir. Eğer üçgende |AB| = |AC| ise, hem açıortay hem de yükseklik aynı doğrudadır.

Dik üçgenlerde Pisagor bağıntısı en önemli kuraldır: a² + c² = b². Ayrıca Öklid bağıntıları da dik üçgenlerde kullanılır: h² = p·k, b² = k·a, c² = p·a. Bazı özel dik üçgenler vardır: 3-4-5, 5-12-13, 8-15-17 ve 7-24-25 üçgenleri.

İpucu: Dik üçgenler için trigonometrik oranları mutlaka ezberle! sin α = c/b, cos α = a/b, tan α = c/a, cot α = a/c

Daha karmaşık üçgen hesaplamalarında Kosinüs Teoremi $a² = b² + c² - 2bc·cos α$ ve Sinüs Teoremi $a/sin A = b/sin B = c/sin C = 2r$ kullanılır. Bu formüller, dik olmayan üçgenlerde kenar ve açı hesaplamaları yaparken çok işe yarar.

Çokgenler ve Dörtgenler

Çokgenler, geometrinin önemli bir konusudur. n kenarlı bir çokgende, bir köşeden n-3 tane köşegen çizilebilir. Köşegen sayısı $n(n-3)$/2 formülü ile bulunur. Çokgenlerin iç açıları toplamı $n-2$·180° ve dış açı toplamı her zaman 360°dir.

Düzgün çokgenlerde tüm kenarlar ve açılar eşittir. Bir düzgün çokgenin bir iç açısı α = $(n-2)·180°$/n formülü ile bulunurken, bir dış açısı β = 360°/n formülü ile hesaplanır. Önemli bir bağıntı: α + β = 180°.

Dörtgenler çokgenlerin özel bir türüdür. Paralelkenar, karşılıklı kenarları paralel ve eşit olan dörtgendir. Köşegenleri birbirini ortalar ve alanı A = a·b·sin α formülü ile bulunur. Paralelkenarlarda karşılıklı açılar eşittir.

Hatırla: Deltoid şeklinde köşegenler birbirine dik kesişir ve köşegenlerden biri açıortaydır. Bu özellik sorularda sıkça karşına çıkar.

Dikdörtgen, tüm açıları 90° olan paralelkenardır. Köşegenleri eşittir. Kare ise tüm kenarları eşit olan dikdörtgendir. Karelerde köşegenler hem diktir hem de birbirini ortalar. Eşkenar dörtgen ise tüm kenarları eşit olan paralelkenardır. Köşegenler dik kesişir ve açıortaydır.

Çokgenler ve Dörtgenler - Alanlar

Dörtgenlerde alan hesaplamaları birçok şekilde yapılabilir. Paralelkenarlarda A = a·b·sin α formülünü kullanabilirsin. Eğer yükseklik biliniyorsa A = a·h formülü de işe yarar.

Yamukta alan hesabı yapmak için A = $(a+c)/2$·h formülü kullanılır. Burada a ve c paralel kenarlar, h ise yüksekliktir. Bu formül, yamuk alan hesaplamasını dikdörtgen alanına indirgemenin pratik bir yoludur.

Deltoid şeklinde köşegenler birbirine dik kesişir ve alan formülü A = (|AC|·|BD|)/2'dir. Bu formül, deltoidin köşegenlerinin uzunluğu bilindiğinde hızlı çözüm sağlar.

Dikdörtgen için alan formülü A = a·b'dir ve köşegenlerinin uzunluğu |AC| = |BD| = √$a² + b²$ formülü ile hesaplanır.

Önemli: Dörtgenlerde köşegenler birbirini ortalarsa, bu şekil paralelkenardır. Bu özellik, sorularda paralelkenarları tanımlamak için kullanılır.

Karenin alanı A = a² formülü ile hesaplanır ve köşegenlerinin uzunluğu |AC| = |BD| = a·√2'dir. Kare, hem paralelkenar hem dikdörtgen hem de eşkenar dörtgenin özelliklerini taşır. Bu nedenle tüm bu şekillere ait formüller karede de kullanılabilir.

Analitik Geometri - Doğru ve Nokta Analitiği

Analitik geometri, geometri problemlerini koordinat düzleminde cebirsel yöntemlerle çözmeyi sağlar. Eğim kavramı, doğruların analitik geometrideki en önemli özelliğidir. Eğim m = tan α olarak ifade edilir.

İki noktası bilinen doğrunun eğimi m = $y₂-y₁$/$x₂-x₁$ formülü ile hesaplanır. Eğimi m olan ve A(x₁,y₁) noktasından geçen doğrunun denklemi y-y₁ = m$x-x₁$ şeklindedir.

İki nokta arasındaki uzaklık |AB| = √$(x₂-x₁)² + (y₂-y₁)²$ formülü ile bulunur. Bir doğrunun genel denklemi ax + by + c = 0 şeklindedir ve A(x₁,y₁) noktasının bu doğruya uzaklığı h = |ax₁+by₁+c|/√$a²+b²$ formülü ile hesaplanır.

Pratik bilgi: Paralel doğruların eğimleri eşittir $m₁ = m₂$. Birbirine dik doğruların eğimleri çarpımı -1'dir $m₁·m₂ = -1$. Bu bilgi, doğru problemlerinde büyük kolaylık sağlar!

Koordinat düzleminde bir üçgenin alanı A(ABC) = (1/2)·|K-L| formülü ile hesaplanabilir. Burada K ve L değerleri köşe koordinatları kullanılarak bulunur. Bu formül, üçgen alanı hesaplamasında trigonometri bilgisi gerektirmez.

Doğru demeti kavramı ve açıortay doğru denklemleri de analitik geometrinin önemli konularıdır. İki doğrunun açıortay denklemleri, doğru denklemlerinden yola çıkılarak elde edilir ve birbirine dik olma özelliği taşır.

Analitik Geometri - Simetri, Öteleme ve Vektörler

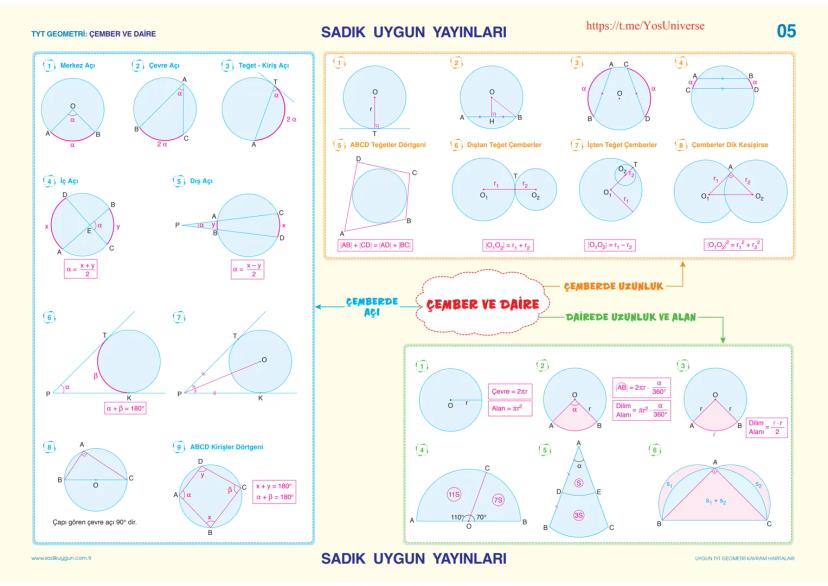
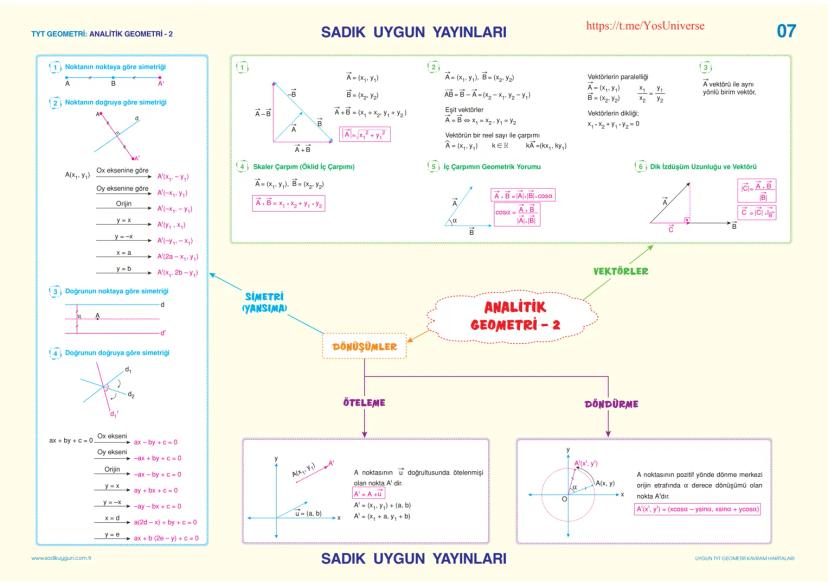
Analitik geometride simetri dönüşümleri, şekillerin belirli eksenler veya noktalara göre yansımalarını inceler. Noktanın Ox eksenine göre simetriği A(x₁,y₁) → A'$x₁,-y₁$, Oy eksenine göre simetriği A'$-x₁,y₁$, orijine göre simetriği ise A'$-x₁,-y₁$ olur.

Doğruların simetri dönüşümlerinde, doğru denkleminin katsayıları uygun şekilde değiştirilir. Örneğin ax+by+c=0 doğrusunun Ox eksenine göre simetriği ax-by+c=0, Oy eksenine göre simetriği -ax+by+c=0 olur.

Öteleme dönüşümünde, bir noktanın koordinatları belirli bir vektör doğrultusunda kaydırılır. A(x₁,y₁) noktasının u=(a,b) vektörü yönünde ötelenmesi ile elde edilen nokta A'$x₁+a,y₁+b$ olur.

Önemli not: Döndürme dönüşümlerinde trigonometrik fonksiyonlar kullanılır. Pozitif yönde α açısı kadar döndürme formülü A(x,y) → A'$xcosα-ysinα, xsinα+ycosα$ şeklindedir.

Vektörlerde temel işlemler toplama, skaler çarpım ve çıkarmadır. İki vektörün toplamı bileşenlerin toplamıdır: A̅+B̅=$x₁+x₂,y₁+y₂$. Skaler çarpım ise A̅·B̅=x₁x₂+y₁y₂ formülü ile hesaplanır.

Vektörlerin paralelliği için x₁/x₂=y₁/y₂ koşulu, dikliği için ise x₁x₂+y₁y₂=0 koşulu gereklidir. Skaler çarpımın geometrik yorumu A̅·B̅=|A̅|·|B̅|·cosα şeklindedir ve iki vektör arasındaki açıyı bulmak için kullanılabilir.