Üçgenler - Temel Kavramlar

Geometri sorularında en sık karşılaştığın şekil olan üçgenler, birçok farklı özelliğe sahip. Dik üçgenlerde Pisagor teoremi $a² + b² = c²$ ve Öklid bağıntıları $h² = p·k$ temel araçların.

Eşkenar üçgenlerde tüm açılar 60°, tüm kenarlar eşit. İkizkenar üçgenlerde ise iki kenar eşit ve bu kenarların karşısındaki açılar da eşit. Bu üçgenlerde yükseklik, açıortay, kenarortay ve simetri ekseni aynı doğru üzerinde bulunur.

Özel üçgenler mutlaka ezberlemen gereken konular: 30°-60°-90° üçgeninde kenar oranları 1:√3:2, 45°-45°-90° üçgeninde 1:1:√2. Ayrıca 3-4-5, 5-12-13, 8-15-17 gibi Pisagor üçlüleri sorularda sık çıkar.

Sınav İpucu: Trigonometri formülleri (sinüs, kosinüs teoremi) ve alan formüllerini $A = ½·a·h = ½·b·c·sinα$ mutlaka ezberle!

Üçgenler - Alan ve Benzerlik

Üçgen alanı hesaplamak için birden fazla yöntem var: A = ½·a·h (taban×yükseklik), A = ½·b·c·sinα (iki kenar arasındaki açıyla), Heron formülü A = √$s(s-a)(s-b)(s-c)$ (üç kenar verildiğinde).

Kenarortaylar ağırlık merkezinde kesişir ve ağırlık merkezi her kenarortayı 2:1 oranında böler. Açıortay teoreminde |BD|/|DC| = |AB|/|AC| oranı çok önemli.

Üçgen benzerliği sorularında A-A-A $açı-açı-açı$ veya K-K-K $kenar-kenar-kenar$ durumlarına dikkat et. Benzer üçgenlerde kenar oranı k ise, alan oranı k², çevre oranı da k olur.

Thales teoremi ve temel benzerlik ile paralel doğrular tarafından oluşturulan orantısal parçalar sınavda sık çıkar. |a/b| = |c/d| orantısını kurabilmen önemli.

Pratik Not: Üçgen eşitsizliğini unutma: |b-c| < a < b+c. Üç kenar verildiğinde üçgen oluşup oluşmadığını kontrol etmek için kullan!

Çokgenler ve Dörtgenler - Temel Özellikler

n kenarlı çokgenlerde köşegen sayısı n$n-3$/2, iç açılar toplamı $n-2$·180°, dış açılar toplamı her zaman 360°. Bu formülleri ezberleyip hızlıca uygulamalısın.

Düzgün çokgenlerde her iç açı $(n-2)·180°$/n, her dış açı 360°/n. Düzgün altıgen sorularında merkezi 6 eşkenar üçgene bölebilirsin - bu çok praktik bir yöntem.

Deltoid (uçurtma şekli) özel bir dörtgen: köşegenleri dik kesişir, bir köşegeni diğerini ortalar ve bir simetri ekseni vardır. Alan formülü A = (d₁·d₂)/2 şeklinde.

Paralelkenar özelliklerini bil: karşılıklı kenarlar eşit ve paralel, karşılıklı açılar eşit, köşegenler birbirini ortalar. Alan = taban×yükseklik = a·b·sinα.

Sınav Taktiği: Düzgün çokgen sorularında merkez açıyı bul $360°/n$, sonra eşkenar üçgenlere böl. Bu yaklaşım çoğu sorunu kolaylaştırır!

Dörtgenler - Özel Şekiller

Kare en özel dörtgen: tüm kenarlar eşit, tüm açılar 90°, köşegenler eşit, dik kesişir ve açıortaydır. Alan = a², köşegen = a√2.

Dikdörtgen ve eşkenar dörtgen (rombus) özelliklerini karıştırma. Dikdörtgende köşegenler eşit, eşkenar dörtgende köşegenler dik kesişir ve açıortaydır.

Yamuk sorularında orta segment özelliği çok önemli: EF = $a+c$/2. İkizkenar yamukta köşegenler eşittir ve h² = a·c bağıntısı geçerli.

Paralelkenar alan formülleri: A = a·h = a·b·sinα. Köşegenler birbirini ortalar ama eşit değildir (kare ve dikdörtgen hariç).

Alan hesaplamalarında hangi formülü kullanacağına karar vermek önemli. Verilen bilgilere göre en pratik yöntemi seç.

Dikkat: Yamuk sorularında hangi kenarların paralel olduğunu mutlaka belirle. Paralellik işareti olan çizgileri gözden kaçırma!

Çember ve Daire

Merkez açı yay uzunluğunu belirler: s = 2πr·(α/360°). Çevre açı merkez açının yarısıdır - bu çok temel bir kural.

Teğet-kiriş açısı teğetin değdiği noktadan başlayıp kirişe kadar olan açıdır. İç açı formülü α = $x+y$/2, dış açı formülü α = $x-y$/2.

Teğetler dörtgeninde karşılıklı kenarlar toplamı eşittir: AB + CD = AD + BC. Bu özellik çok sık kullanılır.

Çemberde uzunluk ve alan: Çevre = 2πr, Alan = πr². Daire dilimi için yay uzunluğu = 2πr·(α/360°), dilim alanı = πr²·(α/360°).

İki çemberin durumları: Dıştan teğet ise merkezler arası uzaklık r₁+r₂, içten teğet ise |r₁-r₂|, dik kesişirse √$r₁²+r₂²$.

Formül Hatırlatması: Çevre açı teoremi sorularda altın kural! Çapa gören çevre açı her zaman 90°'dir.

Analitik Geometri - Doğrular ve Noktalar

Koordinat sisteminde iki nokta arası uzaklık: d = √$(x₂-x₁)² + (y₂-y₁)²$. Orta nokta koordinatları: $(x₁+x₂)/2, (y₁+y₂)/2$.

Doğru denklemi y = mx + n biçiminde. Eğim m = tanα = $y₂-y₁$/$x₂-x₁$. Paralel doğruların eğimleri eşit, dik doğruların eğimleri çarpımı -1.

Noktanın doğruya uzaklığı: h = |ax₁ + by₁ + c|/√$a² + b²$. Bu formül çok sık kullanılır, mutlaka ezberle.

Üçgenin ağırlık merkezi: G$(x₁+x₂+x₃)/3, (y₁+y₂+y₃)/3$. Üçgen alanı koordinatlarla hesaplanabilir - formülü bil.

Açıortay doğrusu iki doğru arasındaki uzaklıkları eşit olan noktaların geometrik yeridir.

Hesap İpucu: Paralel ve dik doğru koşullarını karıştırma! m₁ = m₂ (paralel), m₁·m₂ = -1 (dik).

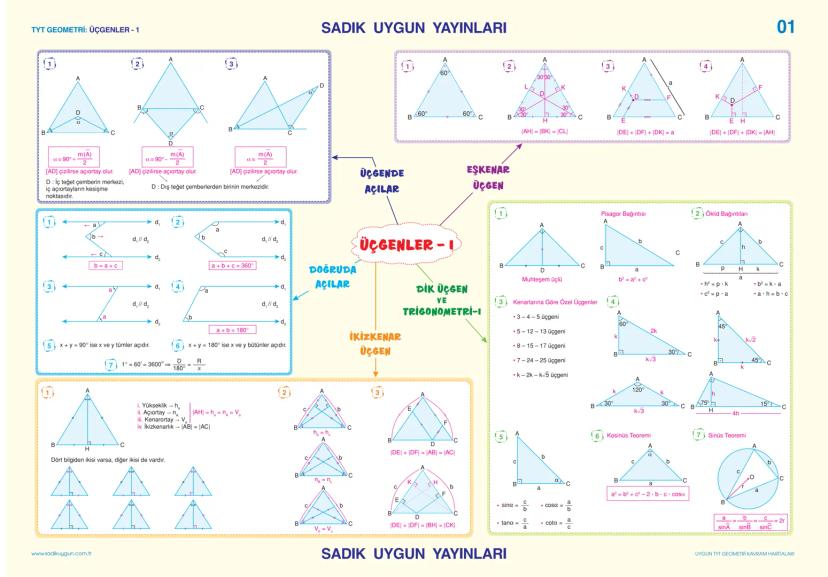
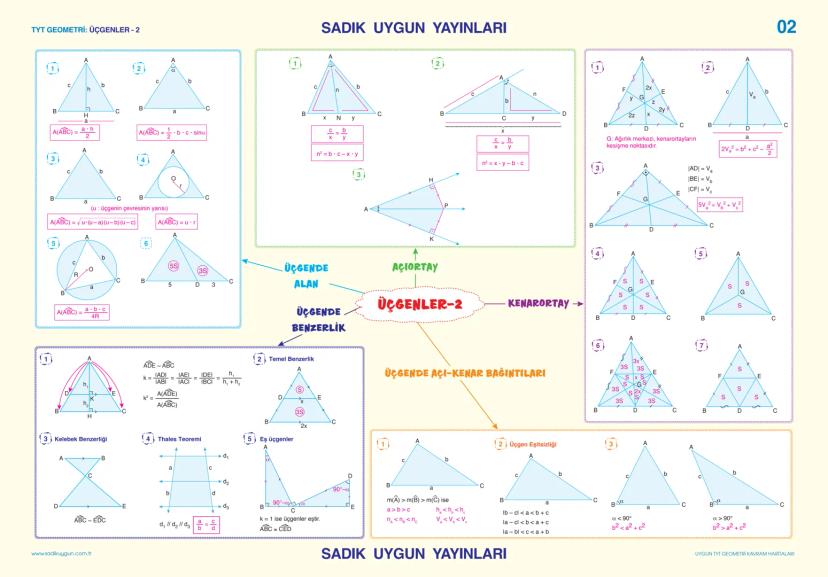
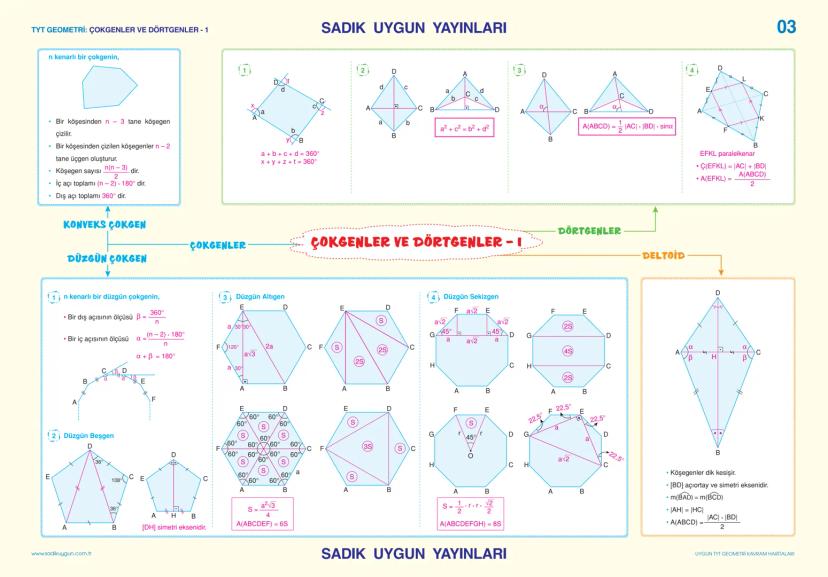
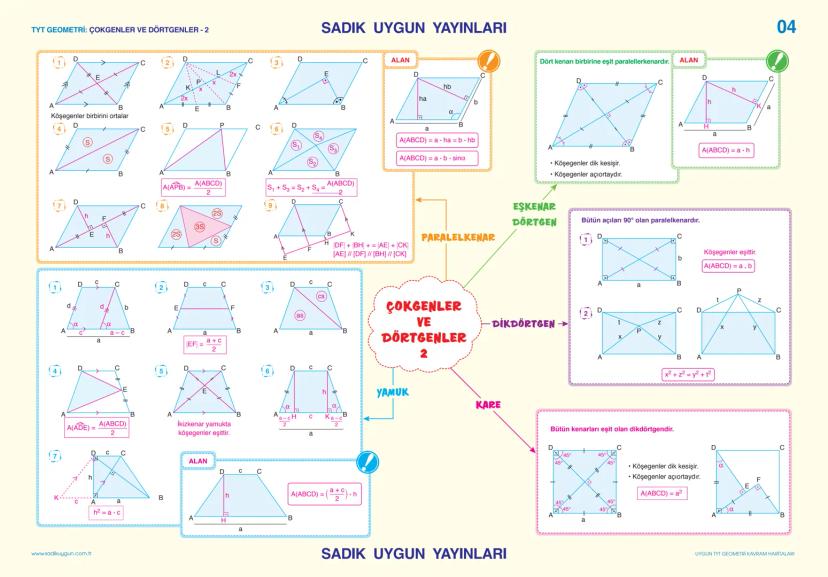
Analitik Geometri - Vektörler ve Dönüşümler

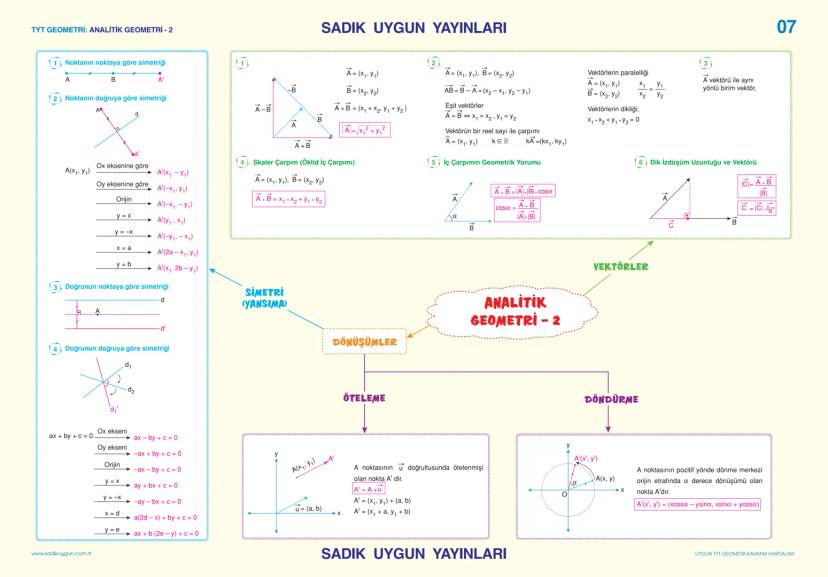
Vektörler yön ve büyüklüğe sahip büyüklüklerdir. İki nokta arası vektör: AB⃗ = $x₂-x₁, y₂-y₁$. Vektör toplamı koordinat koordinat yapılır.

Vektörlerin paralelliği: x₁/x₂ = y₁/y₂. Vektörlerin dikliği: x₁x₂ + y₁y₂ = 0. Bu koşulları sorularda sık kullanırsın.

Skaler çarpım: A⃗·B⃗ = x₁x₂ + y₁y₂ = |A⃗|·|B⃗|·cosα. Açı hesaplamalarında çok pratik.

Simetri dönüşümleri: x eksenine göre $x, -y$, y eksenine göre $-x, y$, orijine göre $-x, -y$. y = x doğrusuna göre (y, x).

Öteleme u⃗ = (a, b) vektörü ile: A'$x₁ + a, y₁ + b$. Dönme α açısı ile: x' = xcosα - ysinα, y' = xsinα + ycosα.

Unutma: Vektörlerde diklik koşulu skaler çarpımın sıfır olması! Bu çok temel ama çok önemli.

Uzay Geometri ve Katı Cisimler

Dikdörtgenler prizmasında cisim köşegeni e = √$a² + b² + c²$, hacim = a·b·c, yüzey alanı = 2$ab + ac + bc$.

Küpte tüm formüller basit: hacim = a³, yüzey alanı = 6a², cisim köşegeni = a√3.

Piramit hacmi = (taban alanı × yükseklik)/3. Koni hacmi = πr²h/3, yanal alanı = πrl (l eğik yükseklik).

Silindir hacmi = πr²h, yüzey alanı = 2πr² + 2πrh. Küre hacmi = 4πR³/3, yüzey alanı = 4πR².

Benzerlik oranları: Uzunluk oranı k ise, alan oranı k², hacim oranı k³. Bu çok önemli bir kural!

Dönel cisimler dikdörtgen (silindir), dik üçgen (koni), daire (küre) döndürülerek oluşur.

Kritik Nokta: Hacim formüllerinde 1/3 katsayısına dikkat et! Piramit ve konide var, prizmada yok.