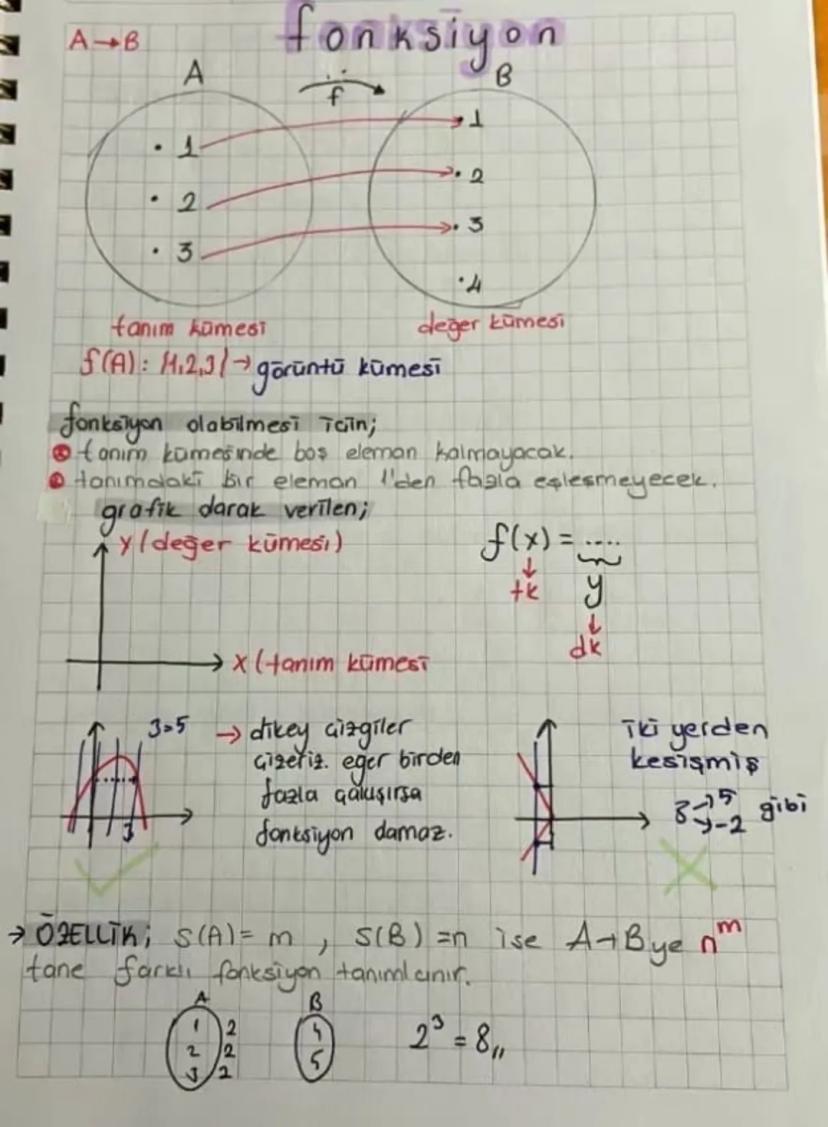
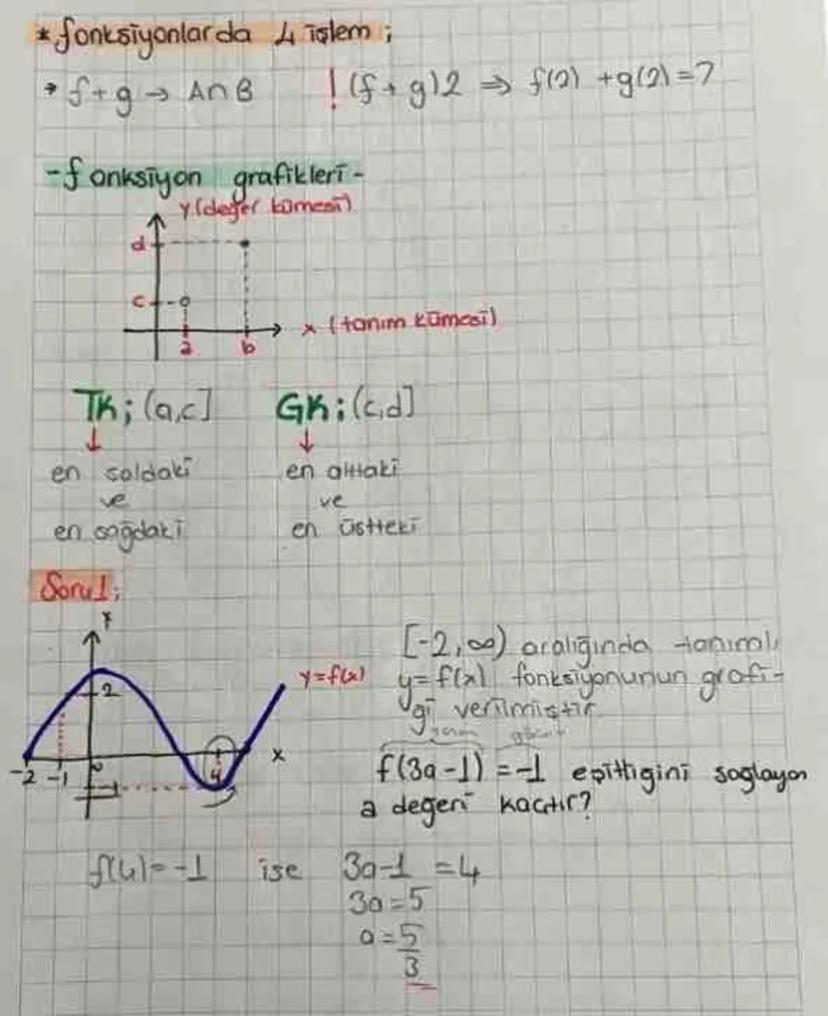
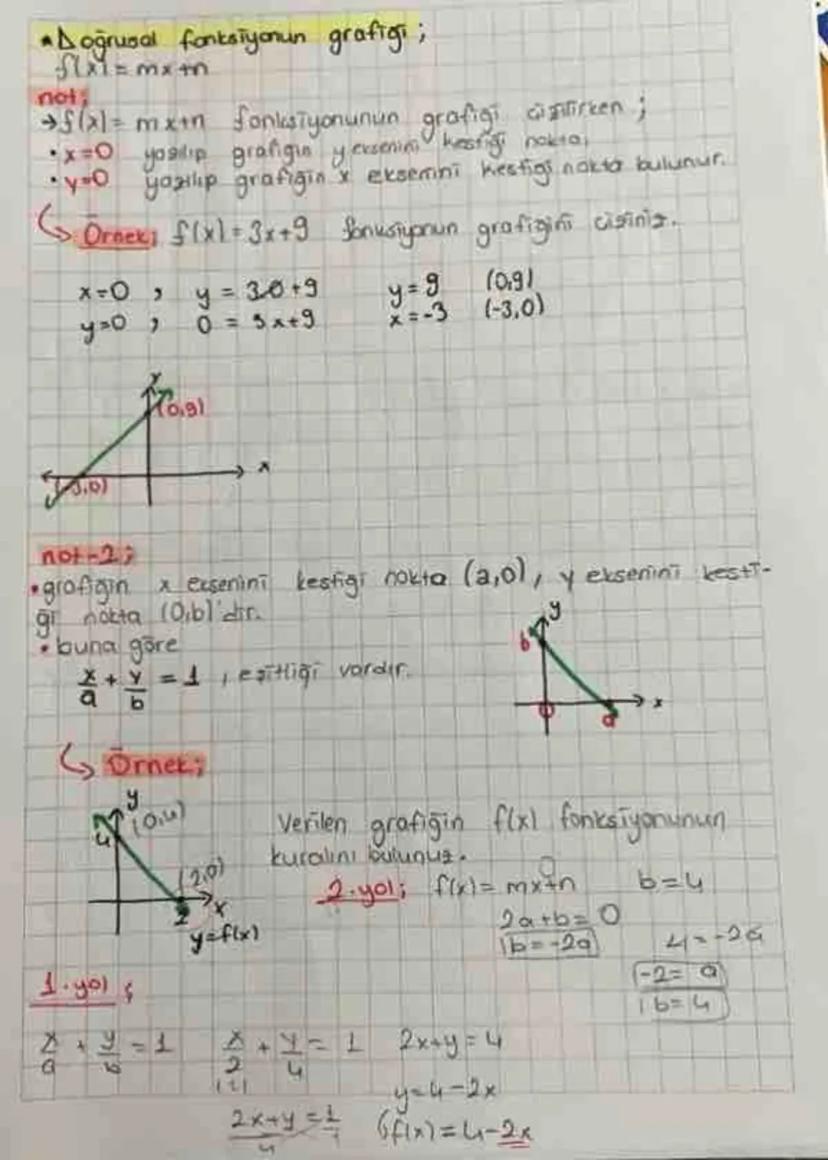
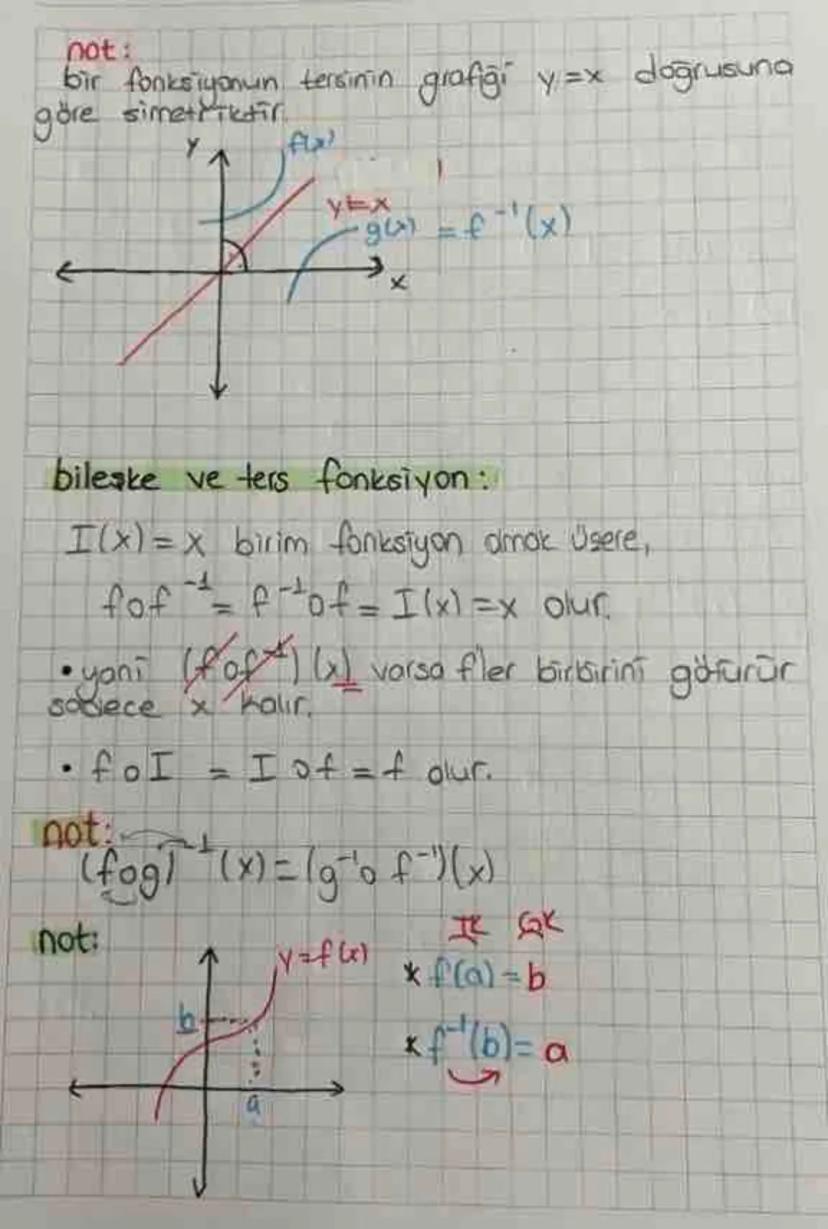
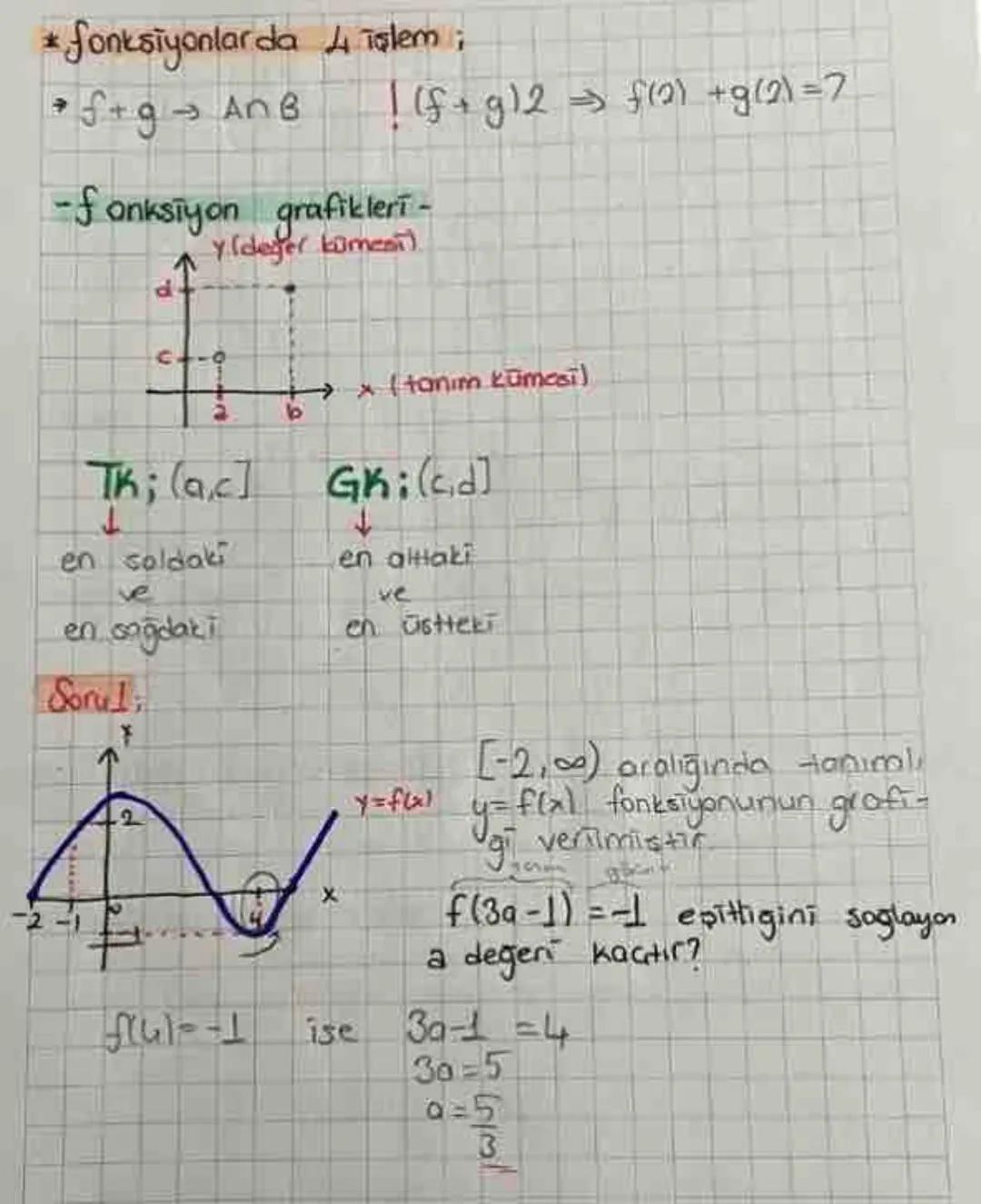
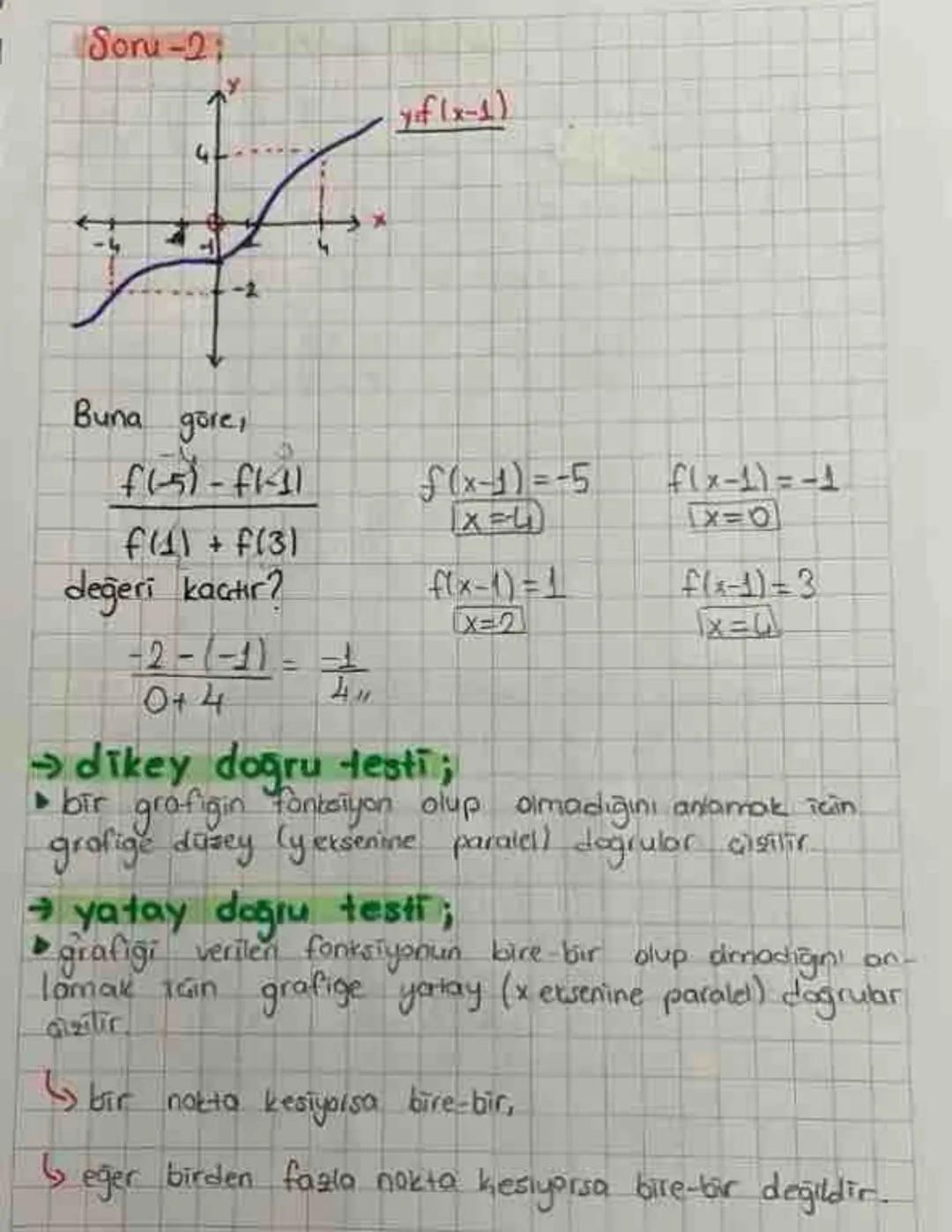
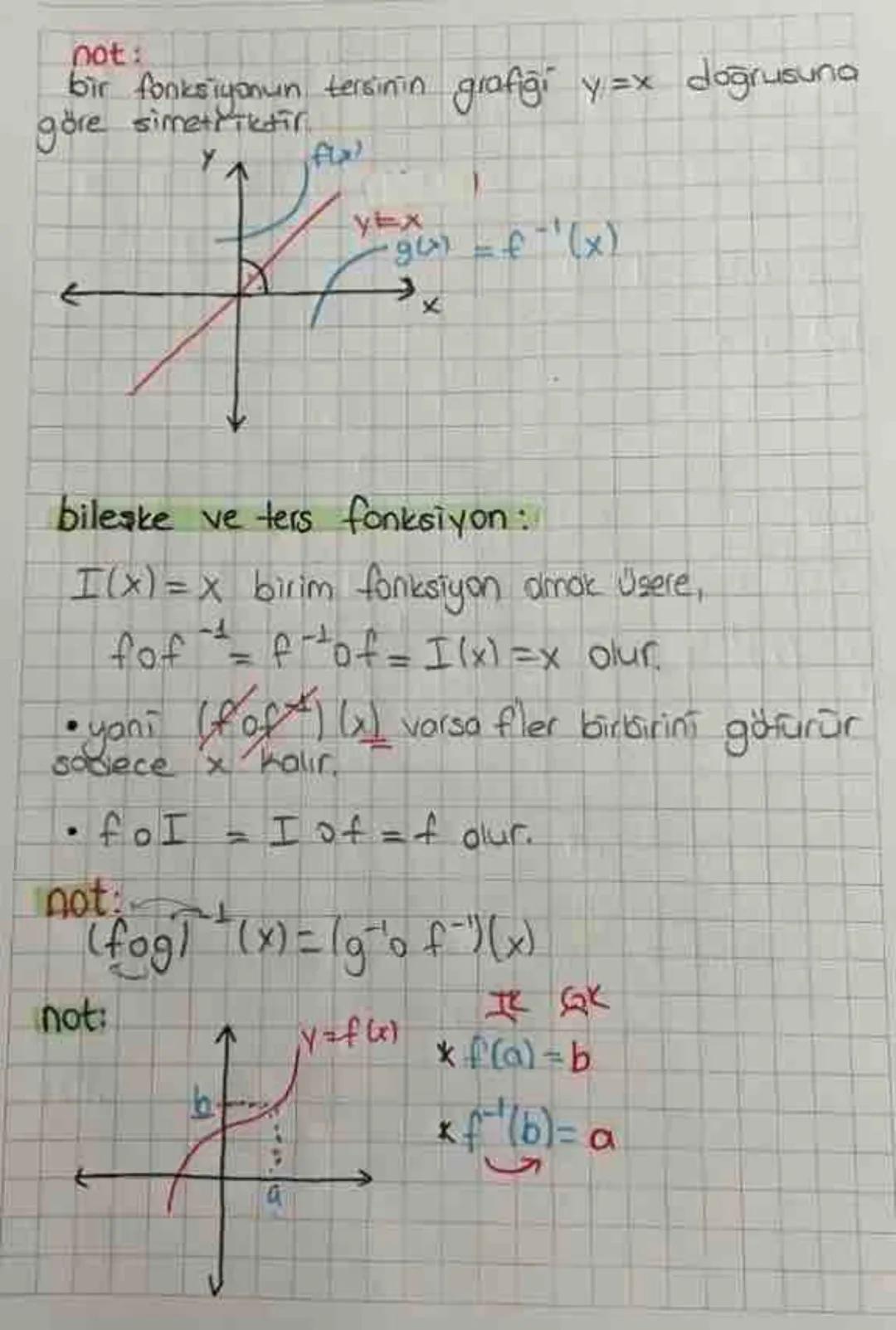
Functions and Their Types- A comprehensive guide covering various... Daha fazla göster
Ders notlarını görmek için kaydolÜcretsiz!
Tüm belgeleri görebilirsin
Notlarını Yükselt
Milyonlarca öğrenciye katıl
Kaydolduğunda Hizmet Şartları ve Gizlilik Politikasını kabul etmiş olursun